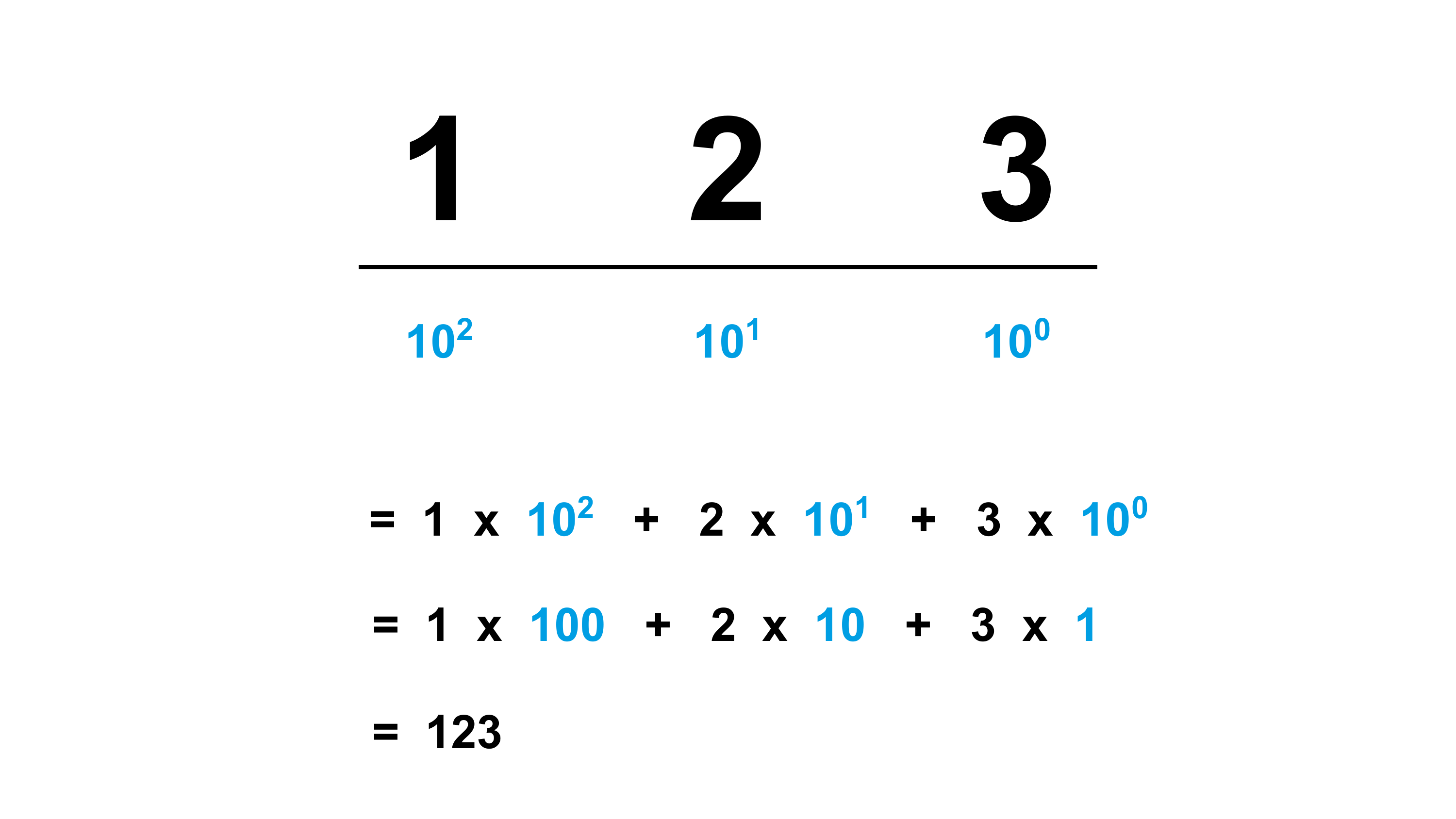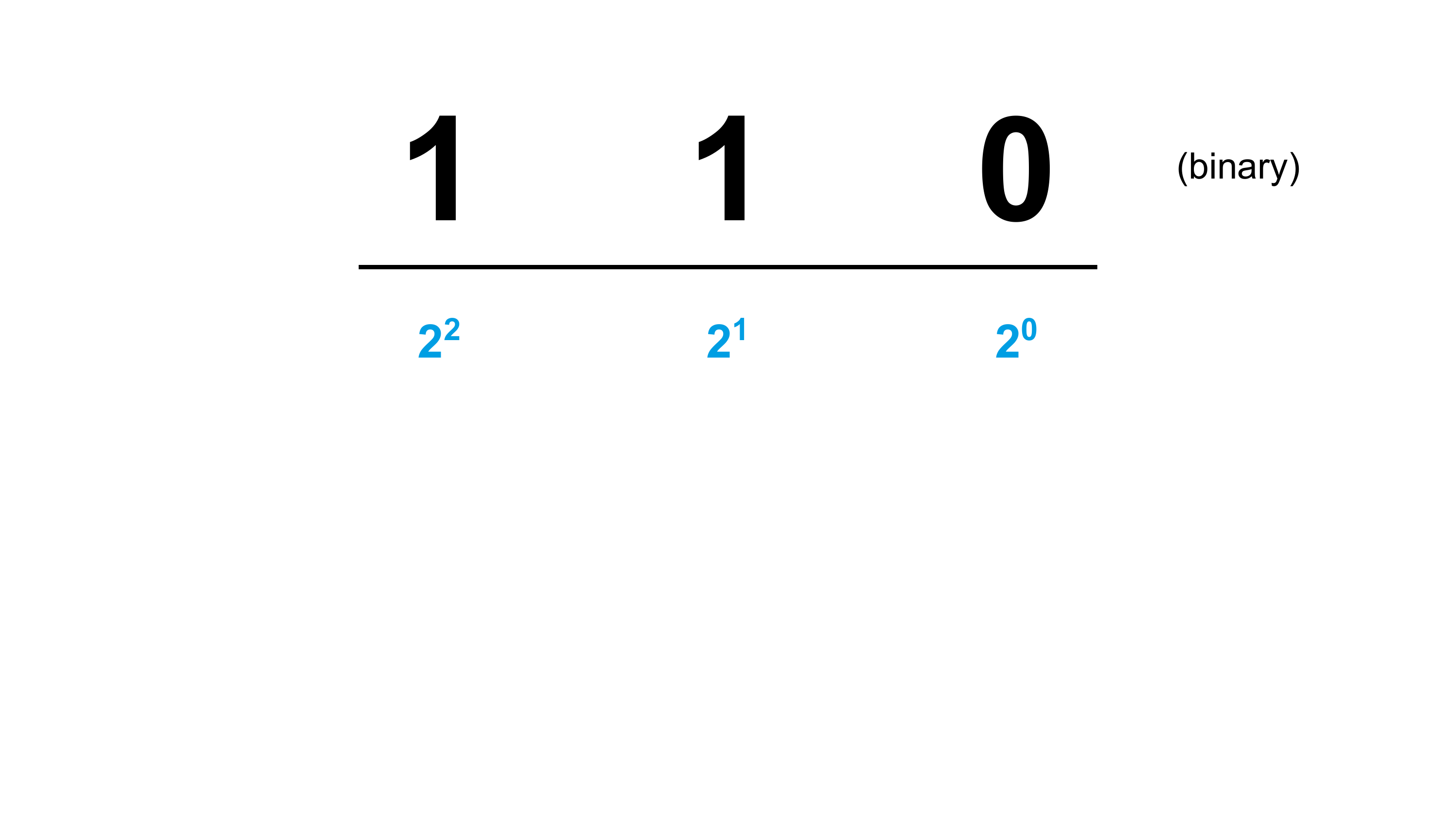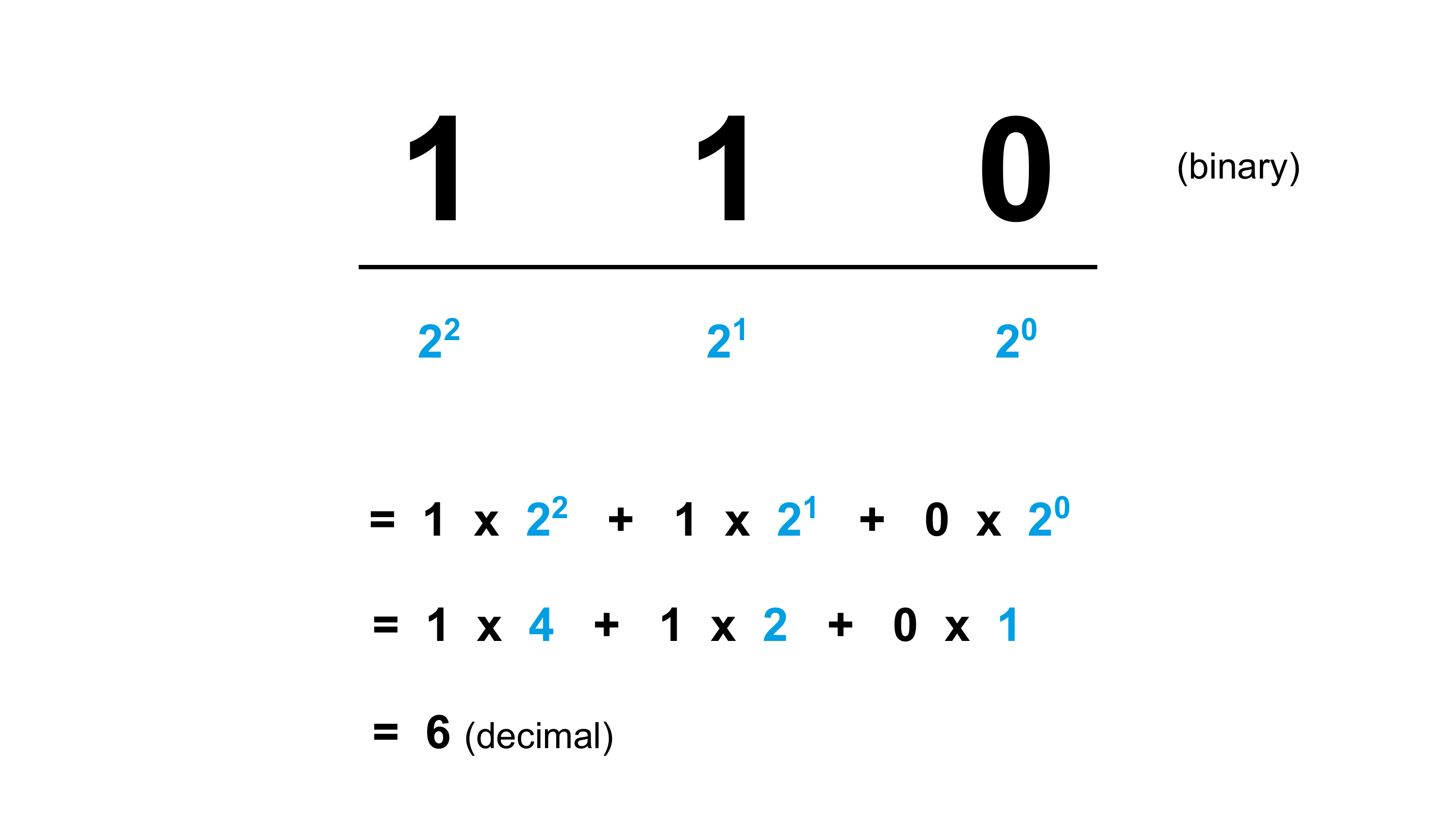- 1
- Wir erstellen eine virtuelle Repräsentation des Drehknopfs in unserem Programm, um seine Funktionen verwenden zu können.
- 2
-
Über die virtuelle Repräsentation des Drehknopfs können wir mittels
get_count()den aktuellen Wert abfragen. Der Parameterresetbestimmt, ob der Zähler nach dem Auslesen zurückgesetzt werden soll oder nicht.
2 Zahlen
Zusammenfassung
Im zweiten Kapitel spendieren wir der LED aus Kapitel 2 eine Dimmfunktion, die wir über einen Drehknopf steuern können.
Auf dem Weg dorthin gehen wir die folgenden Schritte.
| # | Was? | Wo? |
|---|---|---|
| 1 | Wir machen uns mit dem Drehknopf vertraut. | Abschnitt 2.1 |
| 2 | Wir lesen den Zählerstand des Drehknopfs aus einem Programm heraus aus. | Abschnitt 2.2 |
| 3 | Wir führen Kontrollstrukturen ein (if). |
Abschnitt 2.3 |
| 4 | Wir erstellen eine erste Version eines Dimmers für die LED. | Abschnitt 2.4 |
| 5 | Wir beschäftigen uns mit Zahlensystemen. | Abschnitt 2.5 |
| 6 | Wir lernen, was ein Bit und ein Byte ist. | Abschnitt 2.6 |
| 7 | Wir erweitern den LED-Dimmer zur Version 2. | Abschnitt 2.7 |
| 8 | Wir setzen uns mit den Druckknopf auseinander. | Abschnitt 2.8 |
| 9 | Wir bauen Version 3 des LED-Dimmers. | Abschnitt 2.9 |
| 10 | Wir modularisieren unseren Code mit Funktionen. | Abschnitt 2.10 |
2.1 Experimentaufbau
2.1.1 Hardware
Das erste Experiment in Kapitel 1 war ein guter Einstieg! In diesem Kapitel legen wir noch eine Schippe drauf: Unsere Hardware bekommt ein neues Bauteil – einen Drehknopf. Das montiert ihr einfach neben der LED, wie in Abbildung 2.1 gezeigt.
Die vollständige Hardwareliste für dieses Kapitel sieht so aus:
2.1.2 Erste Schritte mit dem Drehknopf
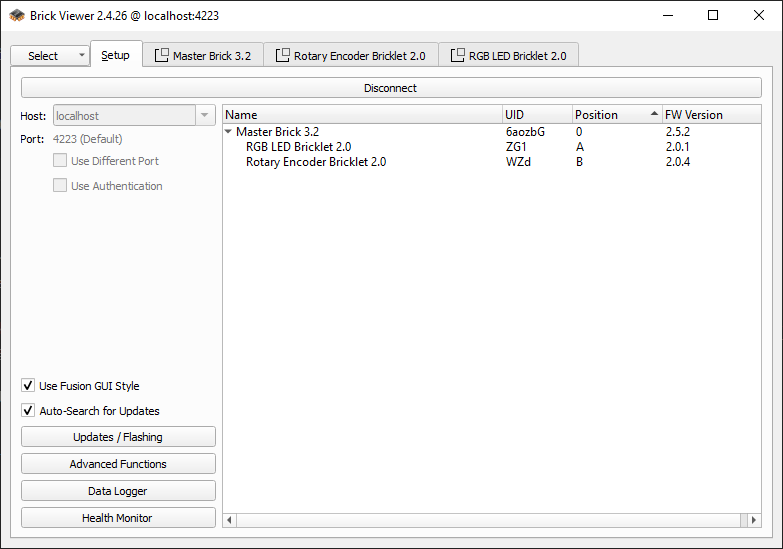
Wie bei der LED werfen wir zuerst einen Blick auf den neuen Drehknopf im Brick Viewer. Schließt dazu euren Master Brick per USB an, startet den Brick Viewer und klickt auf Connect. Im Setup-Tab sollte nun neben der LED auch der Rotary Encoder auftauchen. Denkt daran: Dort findet ihr auch die UID eurer Geräte – die braucht ihr gleich für euer Programm.
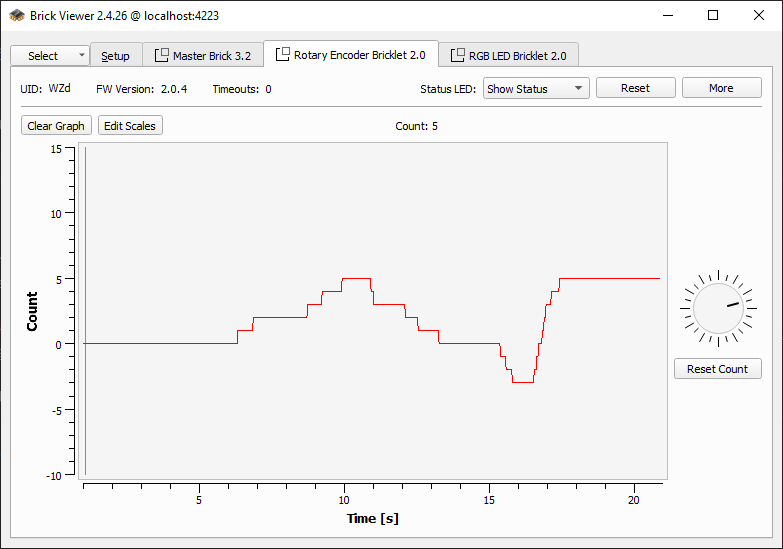
Wechselt nun in den Tab für den Drehknopf, wo ihr ihn direkt testen könnt: Ihr seht den aktuellen Zählwert. Der kann positiv oder negativ sein – je nachdem, wie oft und in welche Richtung ihr gedreht habt. Daneben zeigt ein Diagramm die zeitliche Entwicklung.
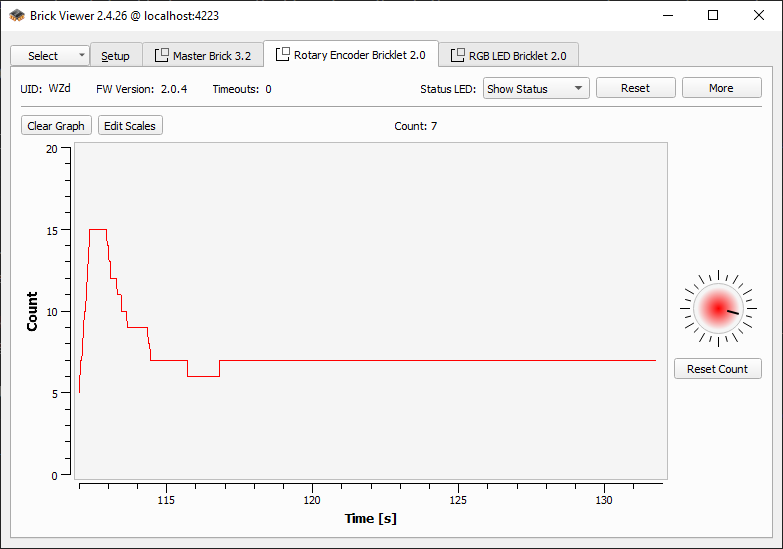
Doch der Knopf kann mehr als nur zählen: Ihr könnt ihn auch drücken. Achtet mal auf den kleinen Kreis im Brick Viewer. Wird er gedrückt, leuchtet er rot. Noch löst das Drücken keine Aktion aus, aber wir überlegen später, welche Funktion wir damit verbinden wollen.
Und zuletzt: der Button Reset Count. Damit setzt ihr den Zähler zurück – eine praktische Funktion, die wir später ebenfalls ins Programm einbauen können.
Fassen wir zusammen, was unser Drehknopf (Rotary Encoder) draufhat:
- Er zählt – vorwärts und rückwärts
- Er merkt, wenn ihr ihn drückt
- Er kann seinen Zähler zurücksetzen
Zeit also, das Ganze in Python auszuprobieren und zu sehen, welche spannenden Anwendungen wir damit bauen können.
2.2 Zähler auslesen
Der Drehknopf funktioniert ähnlich wie der Lautstärkeregler einer Stereoanlage (siehe Abbildung 2.4): Dreht ihr nach rechts, wird es lauter – nach links, leiser.
Im Hintergrund verändert sich bei jeder Drehung der Wert, den der Knopf sendet – mal höher, mal niedriger, je nach Ausgangszustand. Im Brick Viewer habt ihr das schon gesehen. Probieren wir es jetzt in einem Programm aus: Der folgende Code verbindet sich mit dem Drehknopf, liest den aktuellen Wert und gibt ihn in der Konsole aus. Denkt daran, eure eigene UID einzutragen:
Die Ausgabe sollte mit dem Wert übereinstimmen, den ihr auch im Brick Viewer seht – kein Wunder, beide nutzen dieselbe Programmierschnittstelle. Damit habt ihr die erste Funktion des Drehknopfs erfolgreich aus Python getestet.
Dreht ihr den Knopf und startet das Programm erneut, erscheint natürlich ein anderer Wert. Klar! Aber jedes Mal neu starten? Das geht besser. Die Lösung kennt ihr schon aus Kapitel 1: eine Schleife, die das Programm so lange wiederholt, bis wir es beenden:
Zur Erinnerung: while True erzeugt eine Endlosschleife. Normalerweise wollen wir so etwas vermeiden – außer, wir brauchen es genau dafür. Endlosschleifen sind praktisch, wenn wir kontinuierlich Daten lesen oder auf Ereignisse warten. Und keine Sorge: Mit Strg+C könnt ihr das Programm jederzeit beenden, wenn die Konsole aktiv ist. Klickt also einmal in die Konsole und drückt Strg+C, dann hat der Spuk ein Ende.
Wenn ihr das Programm ausführt, werdet ihr direkt ein Problem erkennen. Die Schleife rennt förmlich und gibt nacheinander immer wieder denselben Wert aus. Nur wenn wir am Knopf drehen, ändert sich der Wert – wird aber von der Schleife x-mal auf die Konsole geschrieben. Wie könnten wir das verbessern?
2.3 Kontrollstrukturen
Wie wäre es hiermit?
Gehen wir durch, was hier passiert: Zuerst weisen wir der Variable last_count vor dem ersten Schleifendurchlauf den Wert None zu. Anschließend wird in jedem Durchlauf der aktuelle Zählerstand ausgelesen und in der Variable new_count gespeichert. Danach prüfen wir, ob sich der neue Wert im Vergleich zum alten unterscheidet. Da last_count im ersten Durchlauf None ist, wird die Bedingung in Zeile 5 beim Start immer True sein. Somit geben wir den Wert zu Beginn auf jeden Fall aus – genau so, wie es für die Anwendung sinnvoll ist.
In den folgenden Schleifendurchläufen wird nur dann etwas ausgegeben, wenn sich der Wert verändert hat, ihr also tatsächlich am Drehknopf gedreht habt. Ansonsten bleibt die Ausgabe unverändert.
Die Prüfung, ob der aktuelle Wert (gespeichert in new_count) sich vom alten Wert unterscheidet, erfolgt in Zeile 5. Hier lernen wir auch ein neues Konzept der Programmierung kennen: die Kontrollstruktur, eingeleitet mit dem Schlüsselwort if, gefolgt von einer Bedingung. Eine Bedingung, kann – wie ihr schon aus Kapitel 1 wisst – nur True oder False sein. Ist sie wahr (True), läuft der eingerückte Code darunter. Ist sie falsch (False), passiert nichts.
Übertragen auf unser Programm heißt das: print(last_count) läuft nur dann, wenn sich der Wert tatsächlich verändert hat. In diesem Fall merken wir uns den neuen Wert und aktualisieren last_count. Beim nächsten Schleifendurchlauf prüfen wir wieder, ob sich etwas getan hat. Meistens ist das nicht so – und genau deshalb sehen wir nur dann eine Ausgabe, wenn wir wirklich am Knopf drehen. Ziemlich effizient, oder?
2.4 LED-Dimmer 1.0
Wenden wir das Gelernte an und bauen einen praktischen LED-Dimmer. Dafür holen wir unsere LED aus Kapitel 1 mit dazu und kombinieren sie mit dem Drehknopf.
Die Idee ist simpel: Der Zähler des Knopfs steuert die Helligkeit der LED. Dreht ihr nach rechts, wird sie heller, nach links, dunkler. Wie bei der Stereoanlage in Abbildung 2.4.
Bevor wir uns an die eigentliche Anwendungslogik machen, brauchen wir Zugriff auf beide Geräte – LED und Drehknopf. Dazu erweitern wir den bekannten Boilerplate-Code und speichern die Geräte in eigenen Variablen:
from tinkerforge.ip_connection import IPConnection
from tinkerforge.bricklet_rotary_encoder_v2 import BrickletRotaryEncoderV2
from tinkerforge.bricklet_rgb_led_v2 import BrickletRGBLEDV2
ipcon = IPConnection()
ipcon.connect("localhost", 4223)
knob = BrickletRotaryEncoderV2("<YOUR_ROTARY_UID>", ipcon)
led = BrickletRGBLEDV2("<YOUR_LED_UID>", ipcon)Dieser Teil muss immer am Anfang unseres Programms stehen, damit alles funktioniert. In den kommenden Beispielen setzen wir ihn als gegeben voraus und wiederholen ihn nicht jedes Mal.
Als Startpunkt nehmen wir den Code von oben, der den Zählerwert auf der Konsole ausgibt. Schließlich brauchen wir genau diese Information – wann sich der Wert ändert und wie er aktuell steht – auch, um die LED zu steuern.
Damit wir die LED von aus bis volle Helligkeit dimmen können, legen wir uns zuerst auf eine Farbe fest. Ich bin zwar kein Fan von weißem LED-Licht, aber für dieses Kapitel ist es am einfachsten: voll aufgedreht leuchtet die LED weiß, ausgedreht ist sie schwarz – klar! Später kümmern wir uns darum, wie wir das Licht wärmer machen können.
Erinnern wir uns also: Was bedeuten die Zustände An und Aus im RGB-Farbraum?
# White
led.set_rgb_value(255, 255, 255)
# Black (off)
led.set_rgb_value(0, 0, 0)Damit haben wir die beiden Extremzustände festgelegt. Doch was passiert dazwischen, wenn die LED gedimmt ist? Ganz einfach: Wir lassen die drei RGB-Werte gemeinsam von 1 bis 255 hoch- oder runterlaufen. Höhere Werte ergeben ein helleres Weiß, niedrigere ein dunkleres.
Setzen wir diese Erkenntnisse in Programmcode um und weisen den Zählerwert den RGB-Werten der LED zu. Spoiler-Alert: Das ist etwas naiv, aber lasst uns mal schauen, was passiert und wo möglicherweise Probleme auftreten:
Lasst es mal laufen und dreht voll auf oder runter! Beobachtet dabei den Wert für last_count. Was passiert, wenn er kleiner als Null wird? Oder wenn er größer als 255 wird? Bumm! Das Programm stürzt ab!
Warum? Auf der Kommandzeile bekommen wir eine lange Fehlermeldung mit der folgenden Aussage ganz am Ende:
struct.error: ubyte format requires 0 <= number <= 255Wenn man die Fehlermeldung googelt oder ChatGPT befragt, bekommt man Hilfe. Offensichtlich wird für einen RGB-Wert, den wir der Funktion set_rgb_value() übergeben, ein bestimmter Datentyp erwartet, der ubyte heißt. Das steht für “unsigned byte” und bedeutet, dass der Wert zwischen 0 und 255 liegen muss.
Moment 🧐 – was hat jetzt das Byte mit 0 bis 255 zu tun? Bisher dachten wir doch, das wäre wegen des RGB-Codes? Stimmt auch, aber der RGB-Code liegt nicht zufällig im Wertebereich von 0 bis 255.
Um das zu verstehen, müssen wir das Binärsystem kennen. Also los!
2.5 Zahlensysteme
Eigentlich ist es schnell erklärt. Das Binärsystem ist wie das Dezimalsystem, mit dem wir alltäglich unterwegs sind – nur nutzt es statt der Basis 10 die Basis 2. Einfach, oder? Wenn nicht, lest weiter – das hier soll schließlich ein Einführungsbuch sein.
2.5.1 Unser Dezimalsystem
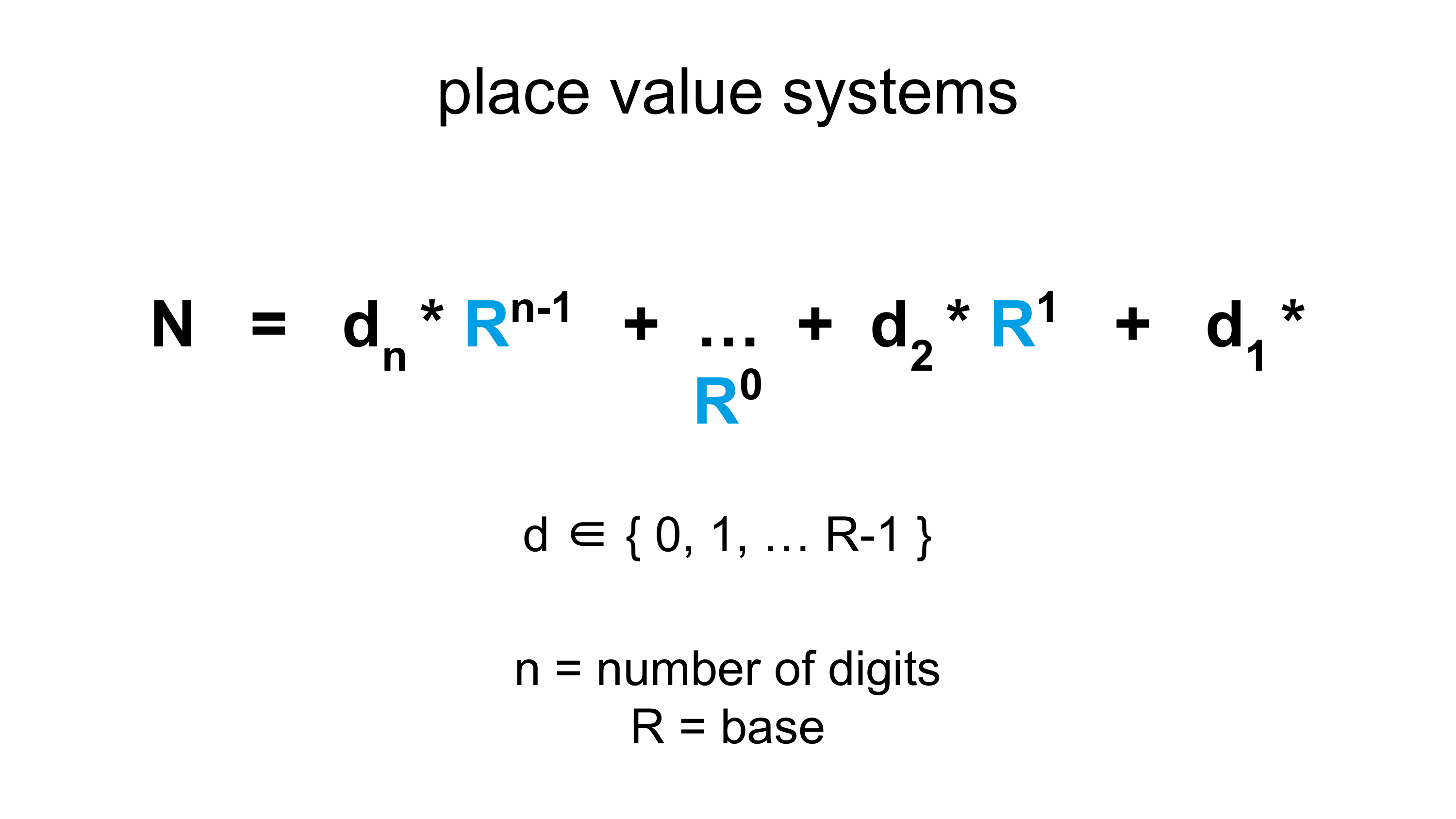
Wir wenden das Dezimalsystem täglich intuitiv an. Es fragt sich wahrscheinlich niemand von euch, was die Systematik dahinter ist, oder? Und doch habt ihr es alle einmal in der Schule gelernt, und wir müssen es an dieser Stelle etwas auffrischen. Solltet ihr mit Stellenwertsystemen noch 100 % vertraut sein, könnt ihr diesen Abschnitt getrost überspringen.
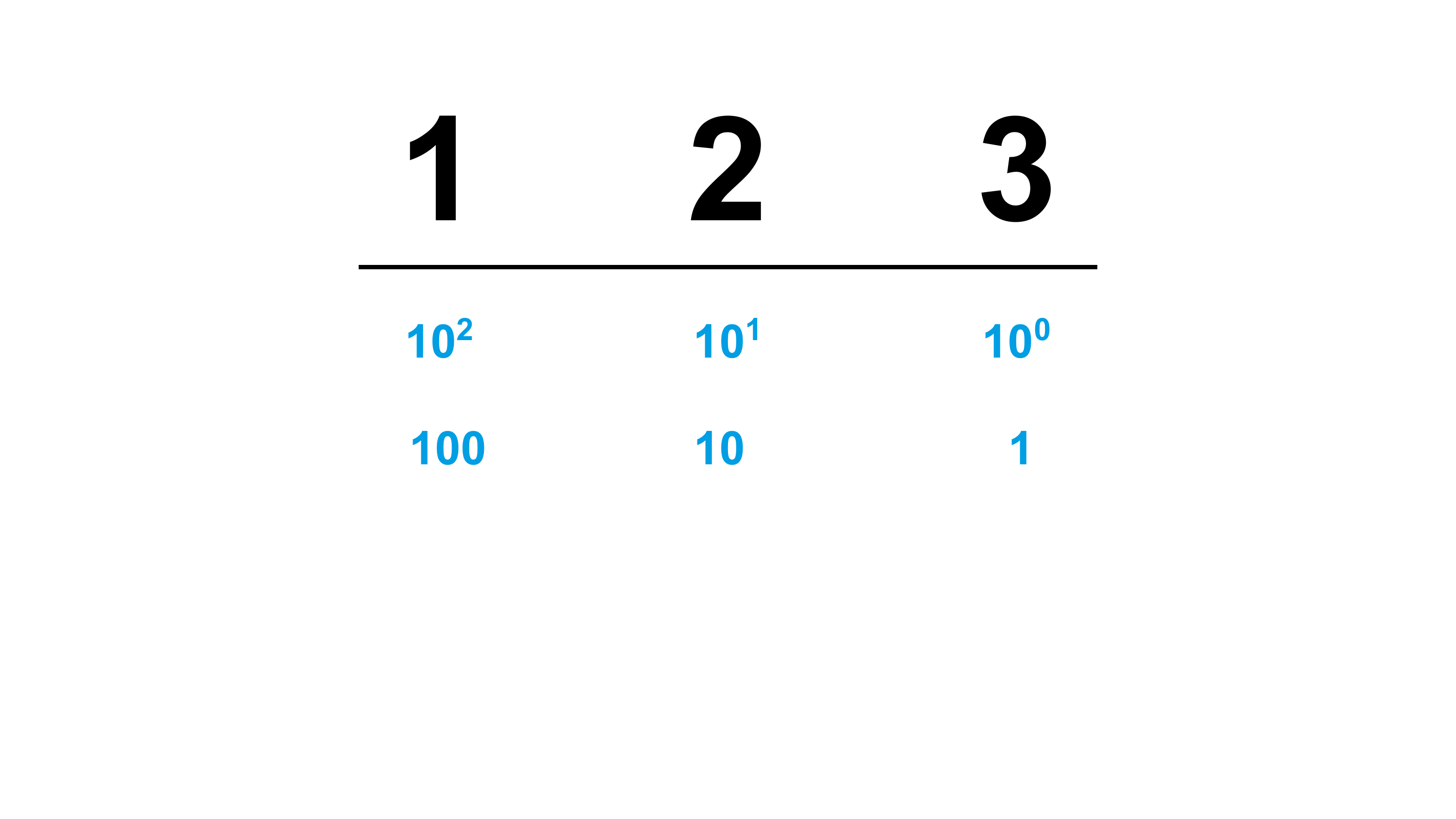
Nehmen wir eine Zahl wie die 123 als Beispiel. Wir haben sofort ein Gefühl für die Zahl, wir wissen etwa, wie groß sie ist. Und wenn wir es etwas genauer erklären müssen, können die meisten von euch sicher erläutern, wofür – also für welchen Wert – jede Ziffer steht. Wir beginnen mit der kleinsten Wertigkeit, also der Ziffer ganz rechts: der 3. Sie steht für die Einserstelle, und davon haben wir 3. Die nächste Stelle steht für die Zehner, und weil dort eine 2 steht, sind es zwanzig. Also \(3+20=23\). Schließen wir auch die dritte und letzte Ziffer in unsere Erläuterung ein: Die 1 steht für die Hunderterstelle, also \(1*100=100\). Damit haben wir \(100+20+3=123\). Ganz einfach und intuitiv.
Das Ganze funktioniert nicht nur mit dreistelligen Zahlen, sondern prinzipiell mit beliebig langen Zahlen. Wir wissen, dass die nächste Ziffer, die wir links im Beispiel in Abbildung 2.6 sehen, für die Tausenderstelle steht. Die nächste Stelle würde für die Zehntausenderstelle stehen – und so weiter. Warum fällt es uns so leicht?
Erstens, weil wir damit jeden Tag umgehen. Das Dezimalsystem ist das System, das wir am häufigsten verwenden, und wir haben es von klein auf gelernt. Es ist intuitiv und einfach zu verstehen. Zweitens aber auch, weil wir die Systematik kennen: Jede Stelle ist 10-mal so viel wert wie die vorherige.
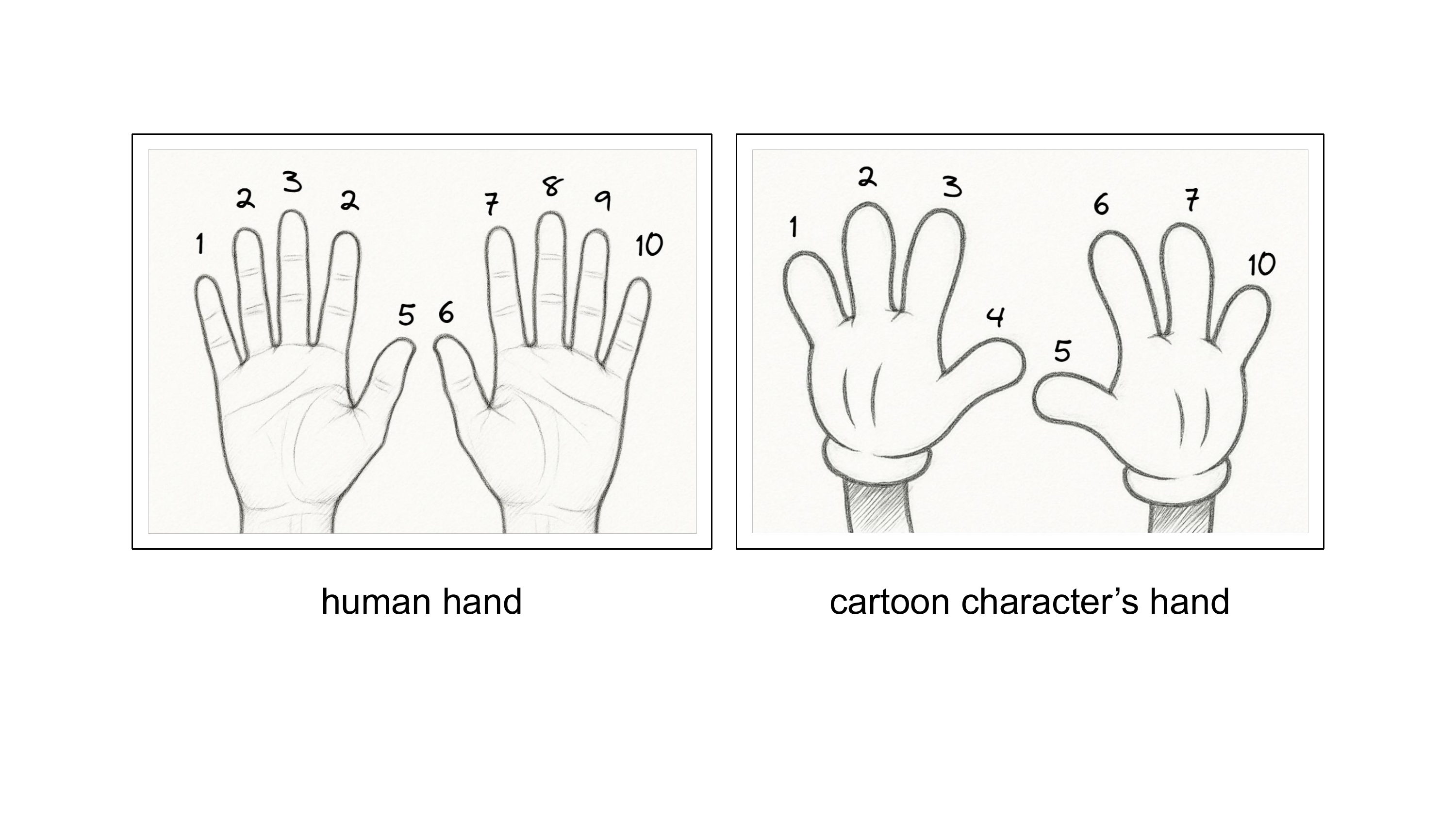
Wurde uns das Dezimalsystem von Gott gegeben? Vielleicht – wenn man an die Schöpfung glaubt1 und daran, dass Gott uns so geschaffen hat, wie wir sind, dann hat er implizit dafür gesorgt, dass wir dezimal denkende Wesen werden. Warum? Eine Theorie besagt, dass die menschliche Anatomie, insbesondere die Anzahl der Finger, einen Einfluss auf unser Zahlensystem hatte. Zählt einfach mal anhand eurer Finger durch.
2.5.2 Das Oktalsystem
Nun gibt es auch Wesen mit weniger als zehn Fingern (und auch mit mehr?). Nehmt mal einen Cartoon-Charakter wie Mickey Mouse als Beispiel. In Abbildung 2.7 seht ihr, wie hier wahrscheinlich gezählt wird. Hätte ein Volk von Mickey-Mäusen sich auch für das Dezimalsystem entschieden?
Vermutlich nicht! Das Oktalsystem ist wie das Dezimalsystem ein Stellenwertsystem, nur mit einer anderen Basis. Das bedeutet, dass jede Stelle statt eine Zehnerpotenz eine Achterpotenz darstellt. Die verfügbaren Symbole oder Zifferen sind 0 bis 7. Warum? Weil es nur acht Finger gibt, und die mit zehn Fingern ist der achte Finger die Zahl 10. Im Oktalsystem stellt das die Dezimalzahl 8 dar, weil die zweite Ziffer von rechts für die Achterstelle steht.
Die 123, die ihr in Abbildung 2.8 seht, können wir - wie jede Zahl in einem beliebigen Stellenwertsystem - mit dem einfachen Ausmultiplizieren in das Dezimalsystem umrechnen. Die drei ganz rechts steht für \(3 \cdot 1\). Weil jede Zahl hoch Null eine Eins ergibt, steht die erste Stelle steht in jedem System für die Eins. Die zweite Stelle steht für \(8^2\), also für die Achter (also \(2 \cdot 8=16\)) und die dritte Stelle \(8^3\), was Vierunsechszig ergbit. Somit geht sie mit \(1 \cdot 64\) in die Berechnung des Dezimalwertes ein. Zusammen ergibt das \(64+16+3=83\) im Dezimalsystem.
2.5.3 Das Binärsystem
Treiben wir es noch ein wenig weiter auf die Spitze und nehmen ein paar Finger weg – sagen wir bis auf zwei. Dann wären wir vielleicht bei einem Delfin mit zwei Flossen, wie ihr ihn in Abbildung 2.9 seht. Delfine haben sich vermutlich auf ein System geeinigt, das auch für unsere heutigen Computer die Grundlage darstellt: das Binärsystem.
Das Wort “binär” stammt aus dem Lateinischen und bedeutet “paarweise” oder “zu zweit”. Von diesem Wort stammt auch der Name des Stellenwertsystems mit der Basis 2 – und das nicht ohne Grund. Im Binärsystem gibt es für jede Stelle genau zwei Möglichkeiten: 0 oder 1. Ein anderer Begriff ist übrigens Dualsystem, was genau das Gleiche meint. Auch das Wort “dual” kommt von den Römern und heißt so viel wie “zwei enthaltend”.
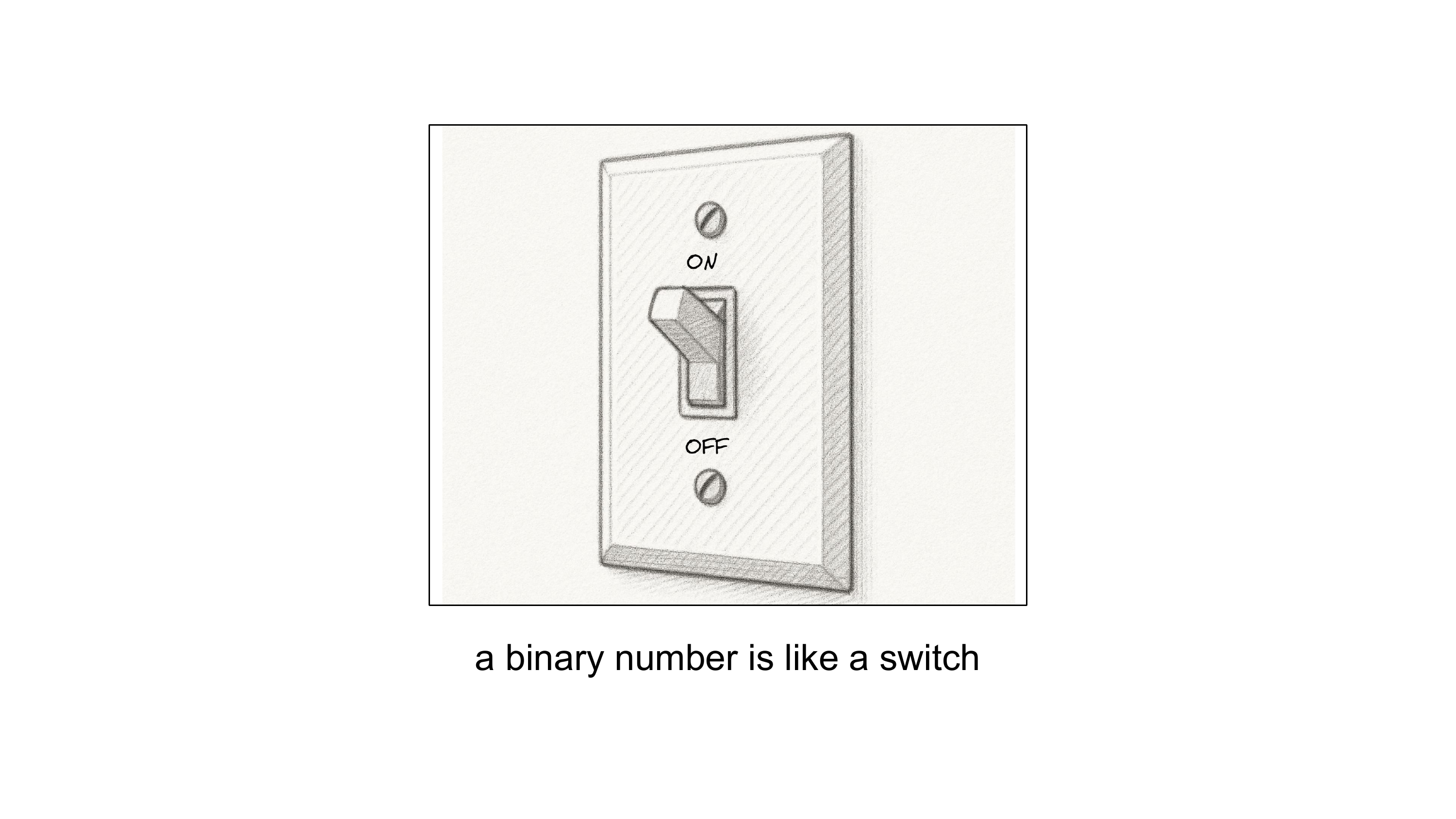
Zwei Möglichkeiten, das erinnert an einen Lichtschalter, der entweder an oder aus sein kann. In Abbildung 2.10 ist das bildlich dargestellt. Entweder leuchtet die Lampe (1) oder sie ist aus (0). Mehr geht nicht. Das Binärsystem ist also wirklich simpel.
Und auch das Rechnen im Binärsystem ist nichts Besonderes. Es funktioniert wie im Dezimalsystem oder Oktalsystem auch, wir tauschen einfach die Basis aus. Jede Stelle stellt nun eine Potenz von zwei dar. Statt vieler Symbole gibt es nur die 0 und die 1, um Zahlen darzustellen. Das macht es im Binärsystem sogar noch einfacher, als in Systemen mit einer höheren Basis. Denn letztlich müssen wir nur die 2er-Potenzen, an denen eine 1 steht, addieren. Alles, wo eine Null steht, können wir ignorieren.
2.5.4 Andere Systeme
Stellenwertsysteme sind nicht die einzigen Zahlensysteme. Es zum Beispiel das römische Zahlensystem, bei dem die Position der Ziffer keine Rolle spielt. Stattdessen werden verschiedene Symbole verwendet, um Zahlen darzustellen. Ein anderes Beispiel ist die Tally-Schreibweise, bei der Striche und Strichpakete verwendet werden, um Zahlen zu darzustellen.
2.6 Bits & Bytes
2.6.1 Zwei Zustände
Warum haben wir uns Zahlensysteme angeschaut, und was hat das mit Computern zu tun? Ganz einfach: Computer denken binär. Das bedeutet, sie kennen nur zwei Zustände: an oder aus, 0 oder 1.
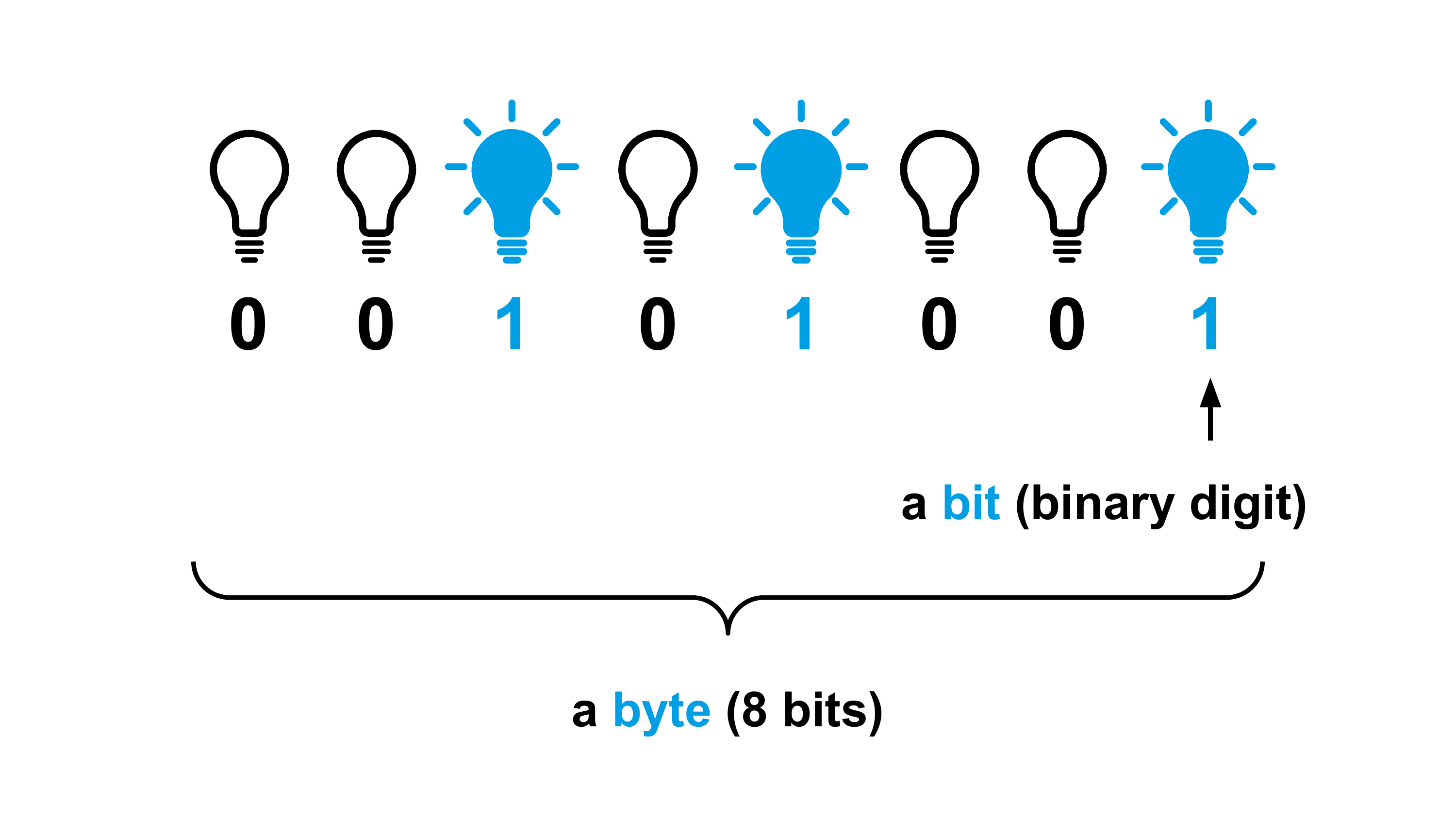
Wir kommen später noch einmal ausführlich darauf zurück, aber so viel schon vorweg: Eine Binärziffer nennen wir im Englischen “binary digit”, kurz “bit”. Jetzt klingelt es, oder?
Ein Bit ist eine Informationseinheit. Nicht irgendeine, sondern die kleinste, die es gibt. Die Erklärung, warum das so ist, folgt später. Wir wollen uns an dieser Stelle die Frage stellen, was wir mit einem Bit alles anstellen können.
Ein Bit ist alleine ziemlich einsam und eingeschränkt. Wenn sich ein Computer mit einem Bit lediglich merken kann, ob eine Lampe an oder aus ist, dann sind das genau zwei Möglichkeiten. Nicht besonders viel. Wir kamen aber von den Farben über Zahlensysteme zu den Bits – und unsere ursprüngliche Frage war, wie ein Computer mit seinen Mitteln – also Nullen und Einsen (oder eben Bits) – so viele unterschiedliche Farben abbilden und speichern kann. Zwei würden gerade einmal für Schwarz/Weiß ausreichen.
Ihr ahnt es vielleicht schon: Wir gesellen zum ersten ein zweites Bit hinzu. Und schon können wir vier unterschiedliche Zustände abbilden: 00, 01, 10 und 11. Damit könnten wir zum Beispiel die Farben Schwarz, Blau, Grün und Cyan darstellen. Etwas willkürlich (warum gerade diese Farben), aber denkbar.
Was passiert, wenn wir ein drittes Bit hinzunehmen? Sind es nun sechs Zustände? Nein, es sind acht: 000, 001, 010, 011, 100, 101, 110 und 111. Damit könnten wir die Farben Schwarz, Blau, Grün, Cyan, Rot, Magenta, Gelb und Weiß darstellen (oder jede andere Kombination, die wir uns wünschen).
Mit jedem zusätzlichen Bit können wir also nicht plus zwei mehr Zustände abbilden, sondern wir verdoppeln unsere Möglichkeiten. Also müssen wir mal zwei – und nicht plus zwei – rechnen. Das ist eine gute Nachricht, denn die Anzahl der Farben, die wir mit jedem zusätzlichen Bit darstellen können, verdoppelt sich jedes Mal.
Das halten wir fest, aber schauen wir zurück auf unsere RGB-Farben und die Fehlermeldung, die wir zuletzt bekommen haben. Der Wert für eine Farbe aus dem RGB-Farbcode muss zwischen 0 und 255 liegen. Wir haben somit inklusive der Null 256 Möglichkeiten für jede der drei RGB-Grundfarben. Wie viele Bits benötigen wir dafür? Rechnen wir es aus:
\[ \begin{aligned} 2^0 &= 1 \\ 2^1 &= 2 \\ 2^2 &= 4 \\ 2^3 &= 8 \\ 2^4 &= 16 \\ 2^5 &= 32 \\ 2^6 &= 64 \\ 2^7 &= 128 \\ 2^8 &= 256 \\ \end{aligned} \]
Stopp! \(2^8 = 256\), das genügt uns völlig. Mit 8 Bits können wir somit 256 Zustände abbilden – genau passend für 256 Rot-, Grün- oder Blauanteile.
2.6.2 Acht Bits macht ein Byte
Und das ist kein Zufall: 8 Bits sind für Computer eine besondere Größe. Wir nennen eine Gruppe von 8 Bits ein Byte. Und jetzt dürfte es erneut klingeln.
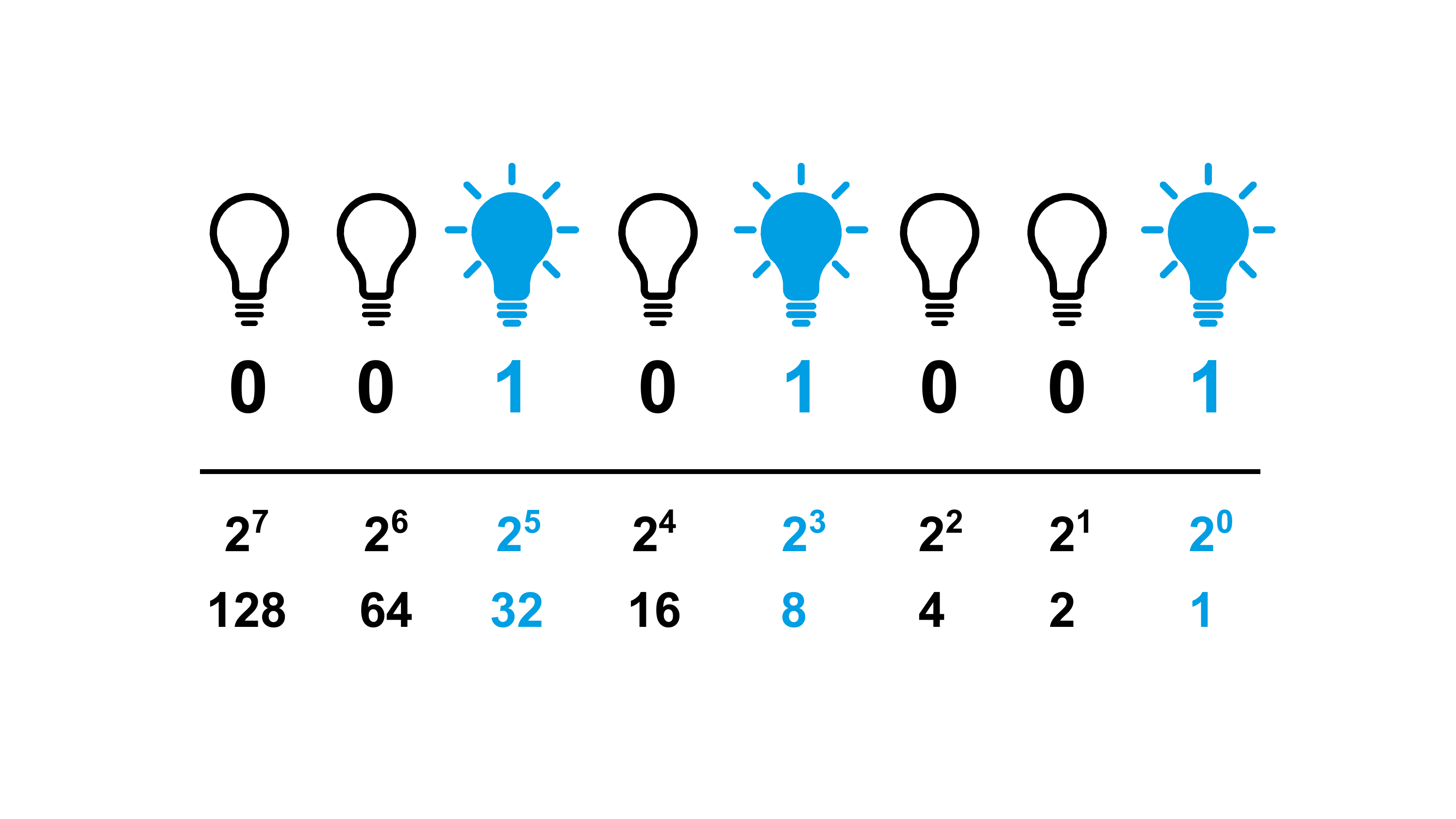
In Abbildung 2.12 ist ein Byte als Reihe von acht Glühbirnen dargestellt. Ihr könnt euch vorstellen, dass Bits mit dem Wert 1 leuchten und Bits mit dem Wert 0 aus sind. Um den Wert zu ermitteln, den das Byte gerade darstellt, könnt ihr jeder Glühbirne von rechts nach links die entsprechenden Wertigkeiten der Stellen aus dem Binärsystem zuweisen und die Werte addieren. Stellen, an denen die Glühbirne leuchtet, werden addiert, die anderen werden ausgelassen (Abbildung 2.13). Das Byte im gezeigten Beispiel steht somit für:
\[ 32 + 8 + 1 = 41 \]
Wofür steht das Byte, wenn alle Lampen leuchten? Oder anders gefragt: Was ist die größte Zahl, die wir mit einem Byte darstellen können?
\[ 128+64+32+16+8+4+2+1 = 255 \]
Die Antwort überrascht uns nicht, denn schließlich haben wir es ja schon herausgefunden: Ein Byte erlaubt uns, Werte zwischen 0 (alle Glühbirnen aus) und 255 (alle Glühbirnen an) darzustellen. Insgesamt also 256 Möglichkeiten. Somit können wir mit 8 Glühbirnen die Intensität einer der drei Grundfarben im RGB-Code darstellen.
Das erklärt auch die Fehlermeldung von oben: Ein Byte kann Werte zwischen 0 und 255 darstellen. Wir haben im Experiment den Drehknopf voll nach oben oder nach unten gedreht, wodurch der Wert entweder größer als 255 oder kleiner als 0 wurde. Und damit ist es kein gültiger Wert im Sinne eines Bytes mehr.
2.6.3 Kilo, Mega, Giga
Ein Byte besteht aus 8 Bits. Wenn wir also von Bytes sprechen, reden wir oft auch von Kilobytes, Megabytes, Gigabytes et cetera. Diese Begriffe sind wichtig, um die Größe von Daten zu beschreiben. In Tabelle 2.1 seht ihr eine Übersicht über die verschiedenen Größenordnungen.
| Potenz (Bytes) | Ausgeschrieben | Bezeichnung (Abkürzung) | Entspricht ca. |
|---|---|---|---|
| \(10^3\) | Tausend | Kilobyte (KB) | kleine Textdatei |
| \(10^6\) | Million | Megabyte (MB) | Digitales Foto |
| \(10^9\) | Milliarde | Gigabyte (GB) | Film (DVD 4,7 GB) |
| \(10^{12}\) | Billion | Terabyte (TB) | Gängige Festplattenkapazität |
| \(10^{15}\) | Billiarde | Petabyte (PB) | Speichervolumen Rechenzentrum |
| \(10^{18}\) | Trillion | Exabyte (EB) | Internetverkehr pro Tag |
| \(10^{21}\) | Trilliarde | Zettabyte (ZB) | Datenbestand weltweit (>100 ZB) |
| \(10^{24}\) | Quadrillion | Yottabyte (YB) | keine Entsprechung |
Jetzt, da ihr wisst, was mit einem Byte gemeint ist, könnt ihr eine ungefähre Vorstellung für die Größenordnungen von Datenmengen entwickeln. Die ersten drei Zeilen aus Tabelle 2.1 könnt ihr selbst einmal nachvollziehen. Schaut euch dazu mal eine Textdatei an, notiert deren Größe und rechnet aus, wie viele Glühbirnen für die Speicherung gebraucht werden. Denkt daran: Ein Byte entspricht acht Glühbirnen.
Wir kommen in den späteren Kapiteln immer wieder auf die Bits und Bytes zurück, weil wir in Computern letztlich überall mit diesen Einheiten arbeiten. Es ist somit gut, wenn ihr schon an dieser Stelle ein grundlegendes Verständnis für diese Konzepte entwickelt.
2.7 LED-Dimmer 2.0
Zurück zu unserem eigentlichen Vorhaben. Wir waren gerade dabei, einen Dimmer für unsere LED zu basteln, als uns die Zahlensysteme dazwischengekommen sind. Dafür haben wir jetzt ein besseres Verständnis dafür, wie ein Computer Farben sieht – nämlich als lange Sequenz aus Nullen und Einsen. Und zwar 24 davon, weil jede Grundfarbe ein Byte an Speicher verwendet.
2.7.1 min() und max()
Was müssen wir also in unserem Programm verändern, jetzt, da wir wissen, was zuvor das Problem war? Genau! Wir müssen sicherstellen, dass die Werte, die wir an die LED senden, im gültigen Bereich für ein Byte liegen – und zwar zwischen 0 und 255.
knob.reset()
last_count = 0
while True:
new_count = knob.get_count(reset=False)
if new_count != last_count:
last_count = new_count
# Clamp last_count to valid byte range
last_count = max(0, min(255, last_count))
print(last_count)
# Setze RGB-Werte auf den Zählerwert
led.set_rgb_value(last_count, last_count, last_count)- 1
-
Die Funktionen
min()undmax()sorgen dafür, dass der Wert vonlast_countimmer zwischen 0 und 255 bleibt. Wennlast_countkleiner als 0 ist, wird er auf 0 gesetzt. Wenn er größer als 255 ist, wird er auf 255 gesetzt.
Die neue Logik in Zeile 11 hilft uns dabei. Nachdem wir den neuen Wert des Zählers in der Variable last_count gespeichert haben (Zeile 8), wenden wir eine geschickte Kombination der beiden Funktionen max() und min() an, um sicherzustellen, dass der Wert im gültigen Bereich bleibt. Wie funktioniert das genau? Dazu gehen wir die Zeile Schritt für Schritt durch.
Zunächst einmal der Ausdruck min(255, last_count). Die Funktion min() gibt einfach den kleineren der beiden Werte zurück, die ihr übergeben werden. Wenn last_count also größer als 255 ist, wird 255 zurückgegeben. Andernfalls wird last_count zurückgegeben. Das Ergebnis dieser Auswertung ist gleichzeitig der zweite Wert, den wir der Funktion max() übergeben.
Die Funktion max() macht genau das Gegenteil. Sie gibt den größeren der beiden ihr übergebenen Werte zurück. Zur Auswahl stehen ihr der Wert 0 und das Ergebnis der min()-Funktion. Das bedeutet, dass max() sicherstellt, dass der endgültige Wert von last_count niemals kleiner als 0 ist.
Und voilà! Nach Zeile 11 kann der Wert von last_count nur noch zwischen 0 und 255 liegen. Problem gelöst!
Probiert es am besten direkt aus und dreht mal voll auf! Es sollte nun kein Fehler mehr auftreten.
2.7.2 Helligkeit entkoppeln
Vielleicht habt ihr es auch bemerkt, aber so richtig toll funktioniert unser Dimmer immer noch nicht. Zwar erscheint keine Fehlermeldung mehr, wenn wir endlos aufdrehen. Jedoch wird die LED auch nicht gedimmt, wenn wir wieder in die andere Richtung drehen. Der Grund dafür ist einfach: Die Helligkeit der LED hängt in unserem Programm direkt vom Zählerstand des Drehknopfes ab. Wenn der über 255 kommt, wird die Helligkeit zwar auf 255 gedeckelt, der Zähler wird aber im Hintergrund trotzdem weiter hochgezählt. Wenn wir die LED wieder dimmen, also einen Helligkeitswert von weniger als 255 erreichen möchten, dann müssen wir zunächst mit dem Drehknopf wieder bis unter die 255 kommen.
Viel schöner wäre es, wenn wir zwar endlos überdrehen könnten, aber mit der ersten Drehung in die andere Richtung die Helligkeit der LED sofort verringern. Ein einfacher Weg wäre, für den Zählerstand des Drehknopfes analog zu last_count nur Werte zwischen 0 und 255 zu erlauben. Dazu könnten wir den Zähler – genau wie last_count – manuell auf 0 oder 255 setzen, je nachdem, ob wir größer als 255 oder kleiner als 0 waren. Leider bietet der Drehknopf über seine Programmierschnittstelle keine solche Funktion an. Wir können den Wert zwar auslesen, aber nicht programmatisch verändern.
Wir müssen also einen Workaround entwickeln. Eine Möglichkeit wäre, die Helligkeit unabhängig vom Zählerstand zu verwalten und dafür eine eigene Variable brightness einzuführen. Wir könnten den Wert von brightness dann erhöhen oder verringern, wenn wir eine Drehung in die eine oder andere Richtung erkannt haben.
Um zu erkennen, ob und in welche Richtung der Drehknopf gedreht wurde, können wir die Differenz zwischen dem aktuellen und dem letzten Zählerstand betrachten. Sie gibt uns direkt Aufschluss: Ist die Differenz positiv, wurde der Knopf nach oben gedreht, ist sie negativ, wurde er nach unten gedreht.
knob.reset()
last_count = 0
brightness = 0
led.set_rgb_value(brightness, brightness, brightness)
while True:
new_count = knob.get_count(reset=False)
if new_count != last_count:
diff = new_count - last_count
last_count = new_count
# Adjust brightness
brightness += diff
brightness = max(0, min(255, brightness))
# Setze RGB-Werte auf den Zählerwert
led.set_rgb_value(brightness, brightness, brightness)
print(f"Brightness / Counter: {brightness} / {new_count}")- 1
-
Die neue Variable
brightnesszu Beginn mit 0 initialisieren. Die LED soll aus sein. - 2
-
Hier ermitteln wir die Differenz zwischen dem aktuellen und dem letzten Zählerstand und speichern sie in der Variable
diff. - 3
-
Wir passen die Helligkeit an, indem wir
brightnessumdifferhöhen oder verringern. Dabei stellen wir sicher, dass der Wert zwischen 0 und 255 bleibt. - 4
- Zur Überprüfung geben wir beide Variablen aus. Wenn wir den Wertebereich 0–255 verlassen, gehen die Werte der beiden Variablen auseinander.
2.7.3 Konstanten
Das sieht schon sehr gut aus! Unser Dimmer ist fast fertig, die grundlegende Funktionalität läuft robust. Eine Kleinigkeit stört mich noch: Der Dimmer reagiert nur sehr langsam, und wir müssen scheinbar endlos drehen, um die LED auf die volle Helligkeit zu bekommen. Können wir das beschleunigen?
Das ist natürlich eine rhetorische Frage – in der Programmierung können wir so gut wie alles umsetzen. Und in diesem Fall ist es sogar recht einfach. Damit die LED schneller hell oder dunkel wird, wenn wir am Drehknopf drehen, können wir die Anpassung der Helligkeit einfach verstärken. Momentan wird die Variable brightness um die Differenz des Zählerstands erhöht oder verringert. Wir könnten stattdessen einen festen, höheren Schrittwert definieren, um die Helligkeit schneller zu ändern.
Dazu definieren wir eine neue Variable, die eine Besonderheit hat. Wir geben ihr den Namen STEP, der nur aus Großbuchstaben besteht (Zeile 3 in Listing 2.1). Gemäß der Regeln für die Bennung von Variablen in Python werden Namen in GROSSBUCHSTABEN üblicherweise für Konstanten verwendet – und tatsächlich ist STEP genau genommen auch keine Variable, sondern eine Konstante.
Eine Konstante unterscheidet sich dadurch, dass ihr Wert einmal festgelegt wird und sich danach nicht mehr ändert. In unserem Fall wollen wir, dass STEP immer den Wert 10 hat. Konstanten definieren wir typischerweise zu Beginn eines Python-Programms, damit man einen schnellen Überblick über alle definierten Konstanten und ihre Werte bekommen kann.
Es ist wichtig zu verstehen, dass der fixe Wert einer Konstante sich nur auf die Ausführung des Programms bezieht. Zwischen mehreren Ausführungen desselben Programms kann der Wert einer Konstante geändert werden. Zum Beispiel könnten wir als Hersteller des LED-Dimmers für eine neue Version entscheiden, dass dieser sich noch schneller dimmen lassen soll, und wir erhöhen den Wert für STEP auf 20. Oder der Benutzer könnte diesen Wert über die Einstellungen der hypothetischen Dimmer-App anpassen.
Wenn wir – wie in Zeile 15 gezeigt – die Differenz des Zählers mit der Schrittgröße multiplizieren, können wir die Anpassung der Helligkeit verstärken.
knob.reset()
brightness = 0
STEP = 10
led.set_rgb_value(brightness, brightness, brightness)
last_count = 0
while True:
new_count = knob.get_count(reset=False)
if new_count != last_count:
diff = new_count - last_count
last_count = new_count
# Adjust brightness
brightness += diff * STEP
brightness = max(0, min(255, brightness))
# Setze RGB-Werte auf den Zählerwert
led.set_rgb_value(brightness, brightness, brightness)
print(f"Brightness / Counter: {brightness} / {new_count}")- 1
-
Hier definieren wir eine Konstante
STEPund weisen ihr den Wert 10 zu. - 2
-
Die Helligkeit wird nun um
diff * STEPangepasst, was bedeutet, dass jede Drehung des Knopfes einen größeren Einfluss auf die Helligkeit hat.
Mit dem LED-Dimmer haben wir die zentrale Funktion des Drehknopfes zur Genüge kennengelernt. Das Gerät hat aber noch eine andere Funktion.
2.9 LED-Dimmer 3.0
Wäre es nicht praktisch, wenn wir das Licht der LED nicht nur dimmen, sondern auch den Farbton verändern könnten? Weißes Licht ist am Abend bekanntlich nicht empfehlenswert, ein wärmerer Farbton verbessert den Schlaf und grünes Licht soll beruhigend wirken.
Lasst uns unseren Dimmer so erweitern, dass per Knopfdruck der Farbton gewechselt werden kann. Fürs Erste wollen wir die Farben Weiß, Gelb und Grün anbieten. Das lässt sich später beliebig erweitern.
2.9.1 Farbe per Variable steuern
Der Ausgangspunkt für unser dimmbares Stimmungslicht ist der Dimmer aus Listing 2.1. Von hier aus fügen wir Schritt für Schritt die Logik für den Farbwechsel per Button ein. Lasst uns aber zunächst ganz ohne Button versuchen, die Farbe der LED zu ändern.
Bisher haben wir es uns einfach gemacht und die LED in Weiß leuchten lassen. Dazu mussten wir nur jeden der drei RGB-Farbkanäle auf den gleichen Wert setzen. Wenn wir neben Weiß auch Gelb und Grün anbieten wollen, müssen wir die Farbkanäle unterschiedlich ansteuern. Für Gelb setzen wir den roten und den grünen Kanal auf den gleichen Wert, während der blaue Kanal auf 0 bleibt. Für Grün setzen wir den grünen Kanal auf den gleichen Wert und die anderen beiden auf 0. Um so eine Logik umzusetzen, haben wir das passende Instrument bereits in unserem Werkzeugkasten: Kontrollstrukturen.
Nehmen wir mal an, wir hätten eine Variable color, auf der die aktuelle Farbe gespeichert ist, in der die LED leuchten soll. Sie könnte also die Werte “white”, “yellow” oder “green” annehmen. Dann könnten wir mit if-Statements die notwendige Logik umsetzen:
Erinnert euch, dass der Code nach einem if nur dann ausgeführt wird, wenn die vorangegangene Bedingung erfüllt ist. Da die Variable color zu einem Zeitpunkt nur einen der drei Werte annehmen kann, muss genau eine der drei Bedingungen erfüllt sein und alle anderen entsprechend nicht.
Wenn wir jetzt zu Beginn unseres Programms color auf einen der drei Werte setzen, können wir die Logik schnell mal testen:
Alles sollte so sein wie zuvor, die LED leuchtet weiß.
Jetzt sollte beim Start des Programms die LED gelb leuchten. Dasselbe probiert mal mit “green” aus, das dürfte auch funktionieren.
2.9.2 Farbe per Knopfdruck ändern
Die aktuelle Farbe in einer Variable zu speichern ist eine gute Idee gewesen. Darauf können wir aufbauen und den Button für den Wechsel der Farbe nutzen. Aber wie?
Zunächst erinnern wir uns an die Logik aus Listing 2.2, in dem wir den Button bereits aus einem Programm heraus getestet haben. Dort haben wir eine Logik gebastelt, die erkennt, wenn der Button gedrückt und wieder losgelassen wird. Wenn das der Fall war, wurde der Wert “Button gedrückt” auf der Konsole ausgegeben. Könnten wir diese Logik nicht verwenden, um statt etwas auszugeben einfach die Farbe zu wechseln?
Natürlich können wir das. Passen wir den Code entsprechend an:
button_pressed_before = False
while True:
button_pressed_after = knob.is_pressed()
if button_pressed_before == True and button_pressed_after == False:
if color == "white":
color = "yellow"
elif color == "yellow":
color = "green"
elif color == "green":
color = "white"
button_pressed_before = button_pressed_afterWieder ein Haufen voller ifs - wir sprechen auch von verschachtelten ifs - aber es sollte funktionieren. Gehen wir es einmal durch: Wenn der Button losgelassen wurde, also das erste if in Zeile 5 True zurückgibt, gelangen wir zur Prüfung des if-Statements auf zweiter Ebene. Hier wird im ersten Fall geprüft, ob die LED gerade Weiß leuchtet (color == "white", Zeile 6). Ist das der Fall, dann wechseln wir jetzt auf Gelb. Im zweiten Schritt sehen wir ein elif (Zeile 8), das sehr ähnlich zu einem if ist, mit der Einschränkung, dass es nur überhaupt geprüft wird, wenn das vorherige if nicht schon wahr war. Das macht in diesem Fall einen großen Unterschied (im Vergleich zu weiter oben, als wir einfache if-Statements verwendet haben, um die Farbe der LED mit set_rgb_color zu setzen). Überlegt mal, was passieren würde, wenn wir hier folgenden Code einsetzen würden:
Geht das mal im Kopf durch. Wenn color aktuell den Wert white hat, dann wird durch das erste if der Wert auf yellow gesetzt. Anschließend wird das zweite if geprüft, das jetzt wahr ist, und der Wert wird auf green gesetzt. Das dritte if wird dann also ebenfalls wahr sein, und der Wert wird wieder auf white gesetzt. Im Endeffekt haben wir also nichts gewonnen, die LED bliebe weiß. Hier ist die Verwendung von elif entscheidend. Denn ein elif wird nur geprüft, wenn das vorherige if oder elif nicht wahr war. Nach der ersten Anpassung wäre hier also Schluss und die Farbe ist wie gewünscht Gelb.
Fügen wir alles zusammen - die neue Logik zum setzen der Farben basierend auf der Varible colorund die Logik zum Ändern der Variable, sowie die Logik des Dimmers aus Listing 2.1:
button_pressed_before = False
# 1. Main loop to keep program running
while True:
new_count = knob.get_count(reset=False)
button_pressed_after = knob.is_pressed()
# 2. Logic for color change on button release
if button_pressed_before == True and button_pressed_after == False:
if color == "white":
color = "yellow"
elif color == "yellow":
color = "green"
elif color == "green":
color = "white"
# Update LED to reflect new color
if color == "white":
led.set_rgb_value(brightness, brightness, brightness)
if color == "yellow":
led.set_rgb_value(brightness, brightness, 0)
if color == "green":
led.set_rgb_value(0, brightness, 0)
button_pressed_before = button_pressed_after
# 3. Logic for brightness adjustment
if new_count != last_count:
diff = new_count - last_count
last_count = new_count
# Adjust brightness
brightness += diff * STEP
brightness = max(0, min(255, brightness))
# Update LED to reflect new color
if color == "white":
led.set_rgb_value(brightness, brightness, brightness)
if color == "yellow":
led.set_rgb_value(brightness, brightness, 0)
if color == "green":
led.set_rgb_value(0, brightness, 0)
print(f"Brightness / Counter: {brightness} / {new_count}")Schaut euch den Code in Ruhe an und prüft, ob ihr ihn Zeile für Zeile nachvollziehen könnt. An dieser Stelle hat unser Programm schon eine beträchtliche Größe angenommen, und so langsam wird es unübersichtlich. Versuchen wir also, Struktur hineinzubringen. Im Wesentlichen besteht das Programm aus drei Teilen, jeden habe ich mit einem vorangestellten Kommentar markiert:
- Hauptschleife, um das Programm am Laufen zu halten
- Logik für Farbwechsel bei Tastenfreigabe
- Logik zur Helligkeitsanpassung
In der Hauptschleife wird am Anfange immer wieder der aktuelle Zählerstand und der Zustand des Buttons abgefragt und auf jeweils einer Variable gespeichert. Diese Werte benötigen wir, um zu entscheiden, ob wir die Farbe ändern oder die Helligkeit anpassen müssen.
Um einen potenziellen Farbwechsel kümmert sich der zweite Block, der mit dem if button_pressed_before == True ... beginnt. Die Bedingung prüft, ob der Button gerade aus dem gedrückten Zustand in den nicht gedrückten Zustand wechselt, der Benutzer ihn also gerade losgelassen hat. In diesem Moment soll die Farbe gewechselt werden. Die Logik dafür haben wir gerade entwickelt.
Um die Helligkeitsanpassung kümmert sich dann der dritte und letzte größere Block. Er beginnt mit if new_count != last_count, was prüft, ob der Drehknop betätigt wurde. Wenn ja, dann wird die Helligkeit entsprechend der Differenz angepasst. Diese Logik haben wir in Abschnitt 2.7 zusammen entwickelt.
Wer von euch jetzt ganz genau hinsieht, der erkennt, dass die Blöcke 2 und 3 zum Teil identischen Code ausführen. In der Programmierung ist das eine rote Flagge 🚩! Lasst uns darüber sprechen, warum!
2.10 Funktionen
In der Programmierung möchten wir Wiederholungen um jeden Preis vermeiden. Wir sprechen auch vom DRY-Prinzip, was für Don’t Repeat Yourself steht. Wenn wir feststellen, dass wir denselben Code an mehreren Stellen verwenden, sollten wir darüber nachdenken, etwas zu verändern. Warum? Und was?
Nehmen wir in unserem Beispiel an, wir führen eine vierte Farbe ein, sagen wir Blau. Dann müssten wir den Code in den Blöcken 2 und 3 anpassen, um die neue Farbe zu berücksichtigen. Das bedeutet, dass wir den gleichen Code an mehreren Stellen ändern müssten, was fehleranfällig und mühsam ist. Zwei mag noch nicht nach einem Problem klingen, aber selbst hier zeigt sich das Problem der Wiederholung. Wird eine Stelle vergessen, ist der Code inkonsistent und funktioniert nicht mehr wie gewünscht.
Die Lösung liegt darin, häufig verwendeten Code in Funktionen auszulagern. Funktionen sind ein mächtiges Werkzeug in der Programmierung. Sie ermöglichen es uns, Codeblöcke zu definieren, die wir immer wieder verwenden können, ohne sie jedes Mal neu schreiben zu müssen. Funktionen helfen uns dabei, unseren Code sauberer, übersichtlicher und wartbarer zu gestalten.
Im Listing 2.3 wird dieser Teil an zwei Stellen wiederholt:
Zeit, diesen Code nur einmal zu schreiben! Machen wir daraus eine Funktion. Wie das geht? Im Prinzip müssen wir vier Dinge klären:
- Was soll die Funktion tun?
- Wie sieht das Ergebnis aus?
- Was benötigt die Funktion, um ihre Aufgabe zu erledigen?
- Wie heisst die Funktion?
In Listing 2.4 seht ihr den fertigen Code für den Dimmer mit Farbwechsel per Knopfdruck.
from tinkerforge.ip_connection import IPConnection
from tinkerforge.bricklet_rotary_encoder_v2 import BrickletRotaryEncoderV2
from tinkerforge.bricklet_rgb_led_v2 import BrickletRGBLEDV2
ipcon = IPConnection()
ipcon.connect("localhost", 4223)
knob = BrickletRotaryEncoderV2("<YOUR_ROTARY_UID>", ipcon)
led = BrickletRGBLEDV2("<YOUR_LED_UID>", ipcon)
knob.reset()
brightness = 0
STEP = 10
led.set_rgb_value(brightness, brightness, brightness)
last_count = 0
color = "white"
button_pressed_before = False
def set_led_color(color, brightness):
if color == "white":
led.set_rgb_value(brightness, brightness, brightness)
if color == "yellow":
led.set_rgb_value(brightness, brightness, 0)
if color == "green":
led.set_rgb_value(0, brightness, 0)
while True:
new_count = knob.get_count(reset=False)
button_pressed_after = knob.is_pressed()
# If button changes from pressed to not pressed
if button_pressed_before == True and button_pressed_after == False:
if color == "white":
color = "yellow"
elif color == "yellow":
color = "green"
elif color == "green":
color = "white"
print(f"Color changed to: {color}")
set_led_color(color, brightness)
button_pressed_before = button_pressed_after
if new_count != last_count:
diff = new_count - last_count
last_count = new_count
# Adjust brightness
brightness += diff * STEP
brightness = max(0, min(255, brightness))
print(f"Brightness / Counter: {brightness} / {new_count}")
set_led_color(color, brightness)Hände hoch, wer daran noch glaubt!↩︎