4  Bilder

Zusammenfassung

In diesem Kapitel arbeiten wir zum ersten Mal mit Bildern auf einem Display. Ausgehend von einem kleinen OLED-Display lernen wir Schritt für Schritt, wie Bilder im Computer repräsentiert werden und wie wir sie programmatisch erzeugen und anzeigen können.

Der Weg dahin führt über folgende Schritte:

# Was? Wo?
1 Wir machen uns mit dem Display vertraut. Abschnitt 4.1
2 Wir lernen das Pixel kennen und schalten es im Display an und aus. Abschnitt 4.2
3 Wir führen die Bitmap als eine Sammlung von Pixelwerten ein. Abschnitt 4.3
4 Wir lernen, wie man Buchstaben als Bitmaps darstellen kann. Abschnitt 4.4
5 Wir lernen eine Alternative zu Bitmaps kennen. Abschnitt 4.5
6 Wir zeigen ein Bild als Bitfolge auf dem Display an. Abschnitt 4.6
7 Wir betrachten Farben in Bitmaps. Abschnitt 4.7
8 Wir lernen, was eine Animation im Computer ist. Abschnitt 4.8
9 Wir wenden einfache Arithmetik auf Bilder an. Abschnitt 4.9
10 Wir animieren Pacman und erwecken ihn auf dem Display zum Leben. Abschnitt 4.10

4.1 Experimentaufbau

4.1.1 Hardware

In den Experimenten dieses Kapitels verwenden wir ein kleines OLED-Display, das wir an unseren Master Brick anschließen. Das Display kann einzelne Pixel weiß aufleuchten lassen und damit einfache Bilder und Texte darstellen. Insgesamt stehen uns 128 × 64 Pixel zur Verfügung, also 8192 einzelne Bildpunkte.

Die vollständige Hardwareliste für dieses Kapitel sieht so aus:

Wenn ihr das Experiment aus Kapitel 3 gemacht habt, dann könnt ihr einfach des OLED-Display hinzufügen und wie in der Abbildung 4.1 gezeigt auf den Master Brick aufschrauben. Die LED und den Infrarotsensor benötigen wir zwar in diesem Experiment nicht, sie stören aber auch nicht.

Abbildung 4.1: Einfaches Setup wie aus Kapitel 3 und erweitert um das OLED-Display.

4.1.2 Das OLED-Display im Brick Viewer

Wie gewohnt starten wir im Brick Viewer. Verbindet euch mit dem Master Brick und ihr solltet die angeschlossenen Geräte sehen können. Den Infrarotsensor kennt ihr bereits aus dem letzten Kapitel. Wir konzentrieren uns hier auf das neue Display im Tab “OLED 128x64 Bricklet 2.0”.

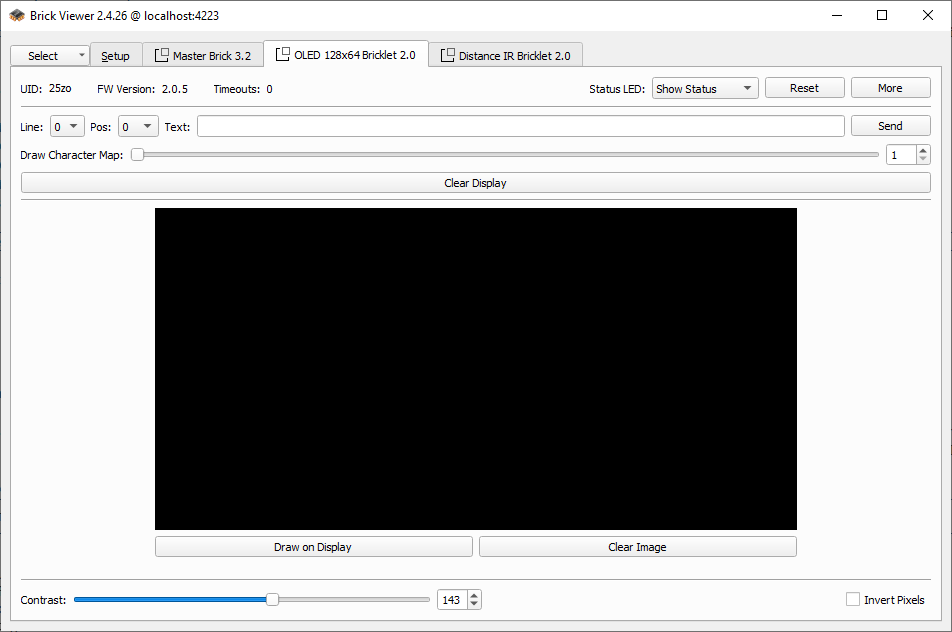
Die Oberfläche für das Display seht ihr in Abbildung 4.2. Im Wesentlichen kann das Display drei Dinge:

  1. Einzelne Pixel ein- und ausschalten
  2. Seinen gesamten Inhalt löschen, also alle Pixel af einmal ausschalten
  3. Text anzeigen (was im Kern nichts anderes ist als ein Spezialfall von 1)

Alle genannten Funktionen könnt ihr direkt im Brick Viewer ausprobieren. Mit der Maus könnt ihr auf der schwarzen Fläche freihändig zeichnen und das Ergebnis mit “Draw on Display” auf das Display übertragen. Mit “Clear Display” löscht ihr den gesamten Inhalt wieder. Alternativ könnt ihr Text in das Textfeld eingeben und mit “Send” anzeigen lassen.

Für Text können wir die Position über die Angabe der Zeile (Line) sowie der Position in der Zeile (Pos) bestimmen. Im Dropdown seht ihr, dass die Zeilen von 0 bis 7 und die Positionen von 0 bis 21 nummeriert sind. Das Display teilt die 128 Pixel Breite in 22 Zeichenpositionen und die 64 Pixel Höhe in 8 Textzeilen auf. Die eingebaute Schrift nutzt ein 5×8-Pixel-Raster pro Zeichen und fügt noch passende Abstände ein.

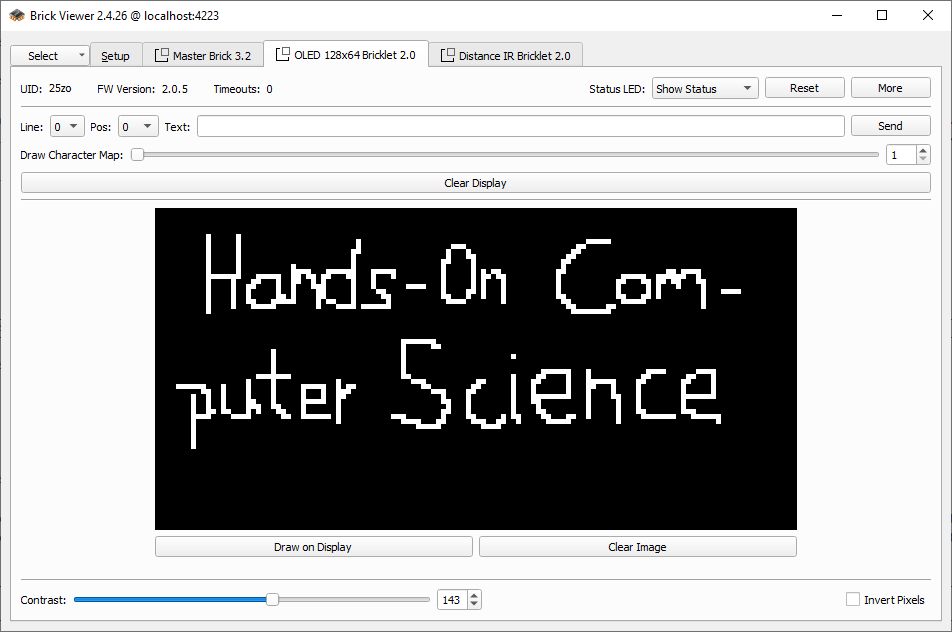
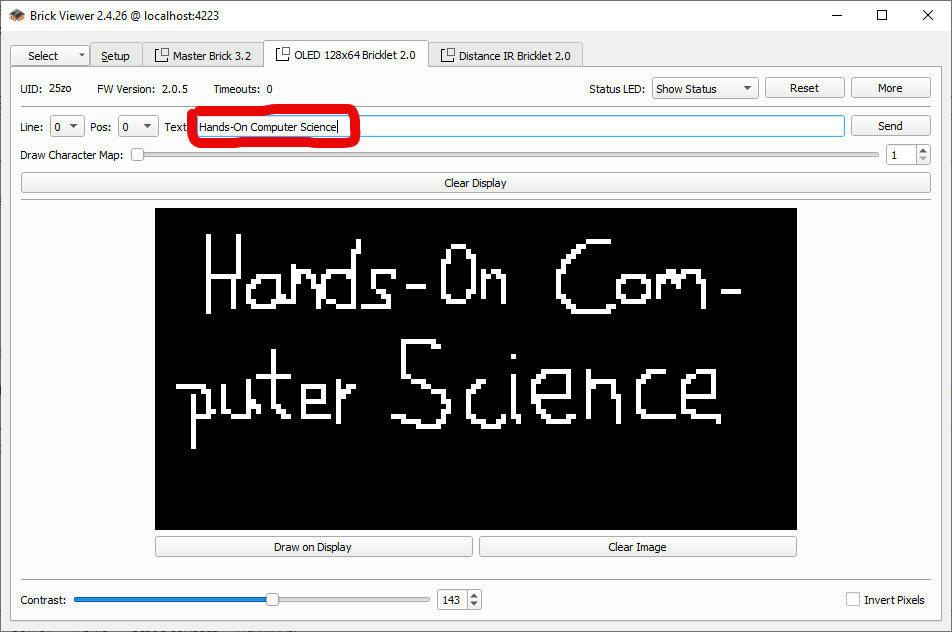
(b) Das Display unterstützt auch die direkte Textausgabe.
Abbildung 4.3

In Abbildung 4.4 könnt ihr den Unterschied zwischen meinem kläglichen Versuch, den Titel des Buches mit der Maus zu zeichnen, und der automatischen Textausgabe sehen. Das Display ist zwar nicht besonders groß, aber für einfache Grafiken und Texte reicht es allemal. Der Text “Hands-On Computer Science” ist aber mit 25 Zeichen zu lang und wird daher abgeschnitten.

(b) Es geht auch direkt als Text, allerdings abgeschnitten.
Abbildung 4.4: Gezeichneter vs. getippter Text auf dem Display.

Was wir im Brick Viewer per Mausklick machen, wollen wir im nächsten Schritt in Python programmatisch steuern.

4.2 Pixel

Nachdem wir das Display im Brick Viewer ausprobiert haben, steuern wir es nun aus Python an. Wie immer stellen wir zuerst die Verbindung her und erzeugen eine Instanz des Display-Objekts. Unser Boilperplate-Code sieht so aus:

from tinkerforge.ip_connection import IPConnection
from tinkerforge.bricklet_oled_128x64_v2 import BrickletOLED128x64V2

ipcon = IPConnection()
ipcon.connect('localhost', 4223)
oled = BrickletOLED128x64V2('25zo', ipcon)
oled.clear_display()
1
Wir importieren die Klasse BrickletOLED128x64V2 aus der Tinkerforge-Bibliothek, die uns die Funktionen des Displays zur Verfügung stellt.
2
Tragt hier eure eigene UID ein.
3
Wir löschen den Display-Inhalt, damit wir mit einem leeren Display starten. Die Funktion clear_display() erledigt das.

Über die Variable oled können wir von nun an die verschiedenen Funktionen des Displays verwenden. Eine davon seht ihr bereits im Codebeispiel, nämlich das Löschen des Displays mit clear_display(). Zu Beginn des Programms ist unser Display somit schwarz.

4.2.1 Was ist ein Pixel?

Das Wort Pixel wird vom englischen “picture element” (Bildelement) abgeleitet. Ein Pixel ist der kleinste darstellbare Punkt auf einem Display.

In unserem Fall kann ein Pixel entweder schwarz oder weiß sein. Auf anderen Bildschirmen, wie dem eures Smartphones oder Fernsehers, können Pixel auch farbig sein. Das schauen wir uns später noch genauer an. In diesem Kapitel konzentrieren wir uns zunächst auf die einfache Schwarzweiß-Darstellung. Auch, weil unser OLED-Display nur Schwarzweiß kann.

Unser Display hat eine Auflösung von 128 × 64 Pixeln. Das bedeutet, dass es 128 Pixel in der Breite und 64 Pixel in der Höhe hat. Insgesamt ergibt das 8192 Pixel, die wir individuell an- oder ausschalten können.

Damit wir mit einzelnen Pixeln sprechen können, hat jedes eine eigene Koordinate, die seine Position als Spalte (x) und Zeile (y) angibt. Genau wie in einer Excel-Tabelle, in der die Zelle in der dritten Spalte und vierten Zeile mit C4 adressiert würde – nur verwenden wir hier statt Buchstaben ausschließlich Zahlen.

Die Koordinaten beginnen bei (0, 0) in der linken oberen Ecke. Die erste Zahl ist die x-Koordinate (horizontal), die zweite die y-Koordinate (vertikal).

4.2.2 Ein einzelnes Pixel setzen

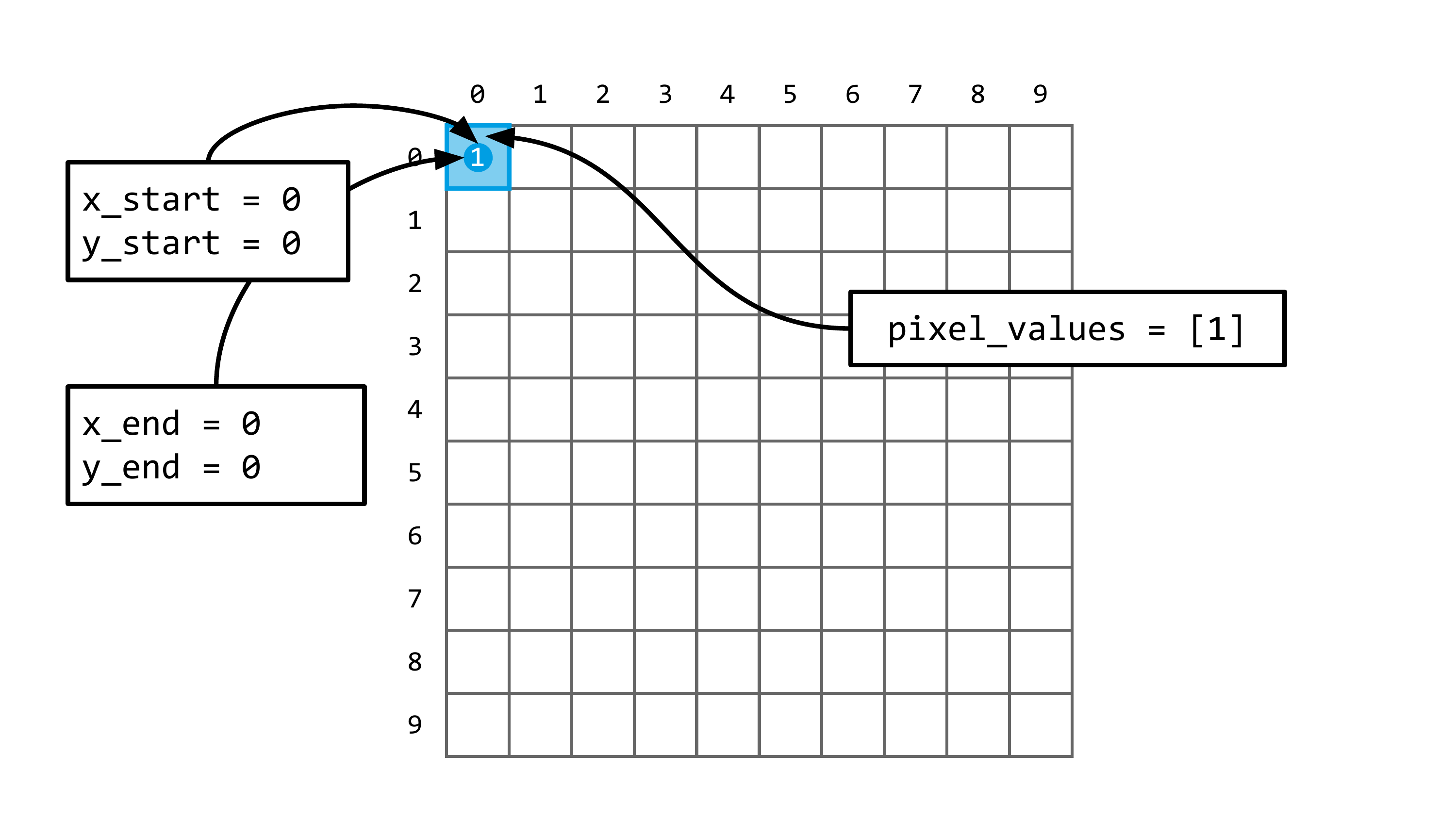
Beginnen wir damit, das Pixel in der linken oberen Ecke des Displays einzuschalten. Dazu verwenden wir die Funktion write_pixels():

oled.write_pixels(0, 0, 0, 0, [1])

Warum so viele Argumente, wenn wir doch nur ein einziges Pixel setzen wollen? Der Grund: write_pixels() kann nicht nur einzelne Pixel, sondern beliebige rechteckige Flächen ansteuern. Die Funktion erwartet deshalb immer die Beschreibung eines Rechtecks plus die zugehörigen Pixelwerte.

Allgemein lautet die Signatur der Funktion so:

write_pixels(x_start, y_start, x_end, y_end, pixel_values)

Die ersten vier Argumente definieren die zwei Eckpunkte des Rechtecks: oben links und unten rechts (beide inklusive). Die Breite ergibt sich aus x_end - x_start + 1, die Höhe aus y_end - y_start + 1.

In unserem Fall sind beide Punkte (0, 0), wir sprechen also genau ein Pixel an. Der letzte Parameter ist eine Liste von Werten, die angibt, ob die Pixel in der definierten Fläche ein- oder ausgeschaltet werden sollen. Ein Wert von 1 bedeutet weiß, 0 bedeutet schwarz. Da wir nur ein Pixel ansprechen, enthält die Liste nur einen Wert: [1].

Auch wenn es im Beispiel nur ein Wert ist, stellt [1] in Python eine Liste dar, darauf weisen die eckigen Klammern hin. Innerhalb der Klammern können beliebig viele Werte durch Kommas getrennt angegeben werden.

Wir können das Pixel wieder ausschalten, indem wir den Wert in der Liste auf 0 ändern:

oled.write_pixels(0, 0, 0, 0, [1])
input("Drücke Enter um das Pixel auszuschalten...")
oled.write_pixels(0, 0, 0, 0, [0])

Einzelne Pixel lassen sich so bequem schalten. Interessant wird es aber erst, wenn wir mehrere Pixel zu einem Bild kombinieren. Das führt uns zu Bitmaps.

4.3 Bitmaps

Eine Bitmap ist nichts anderes als eine rechteckige Matrix von Pixelwerten, die zusammen ein Bild ergeben. Mit write_pixels() können wir solche Rechtecke direkt auf dem Display zeichnen.

4.3.1 Quadrate

Sagen wir, wir wollen ein 2×2 großes Quadrat in der Mitte des Displays zeichnen. Die Mitte des Displays liegt rechnerisch bei (64, 32). Da wir bei 0 zu zählen beginnen, korrigieren wir auf (63, 31).

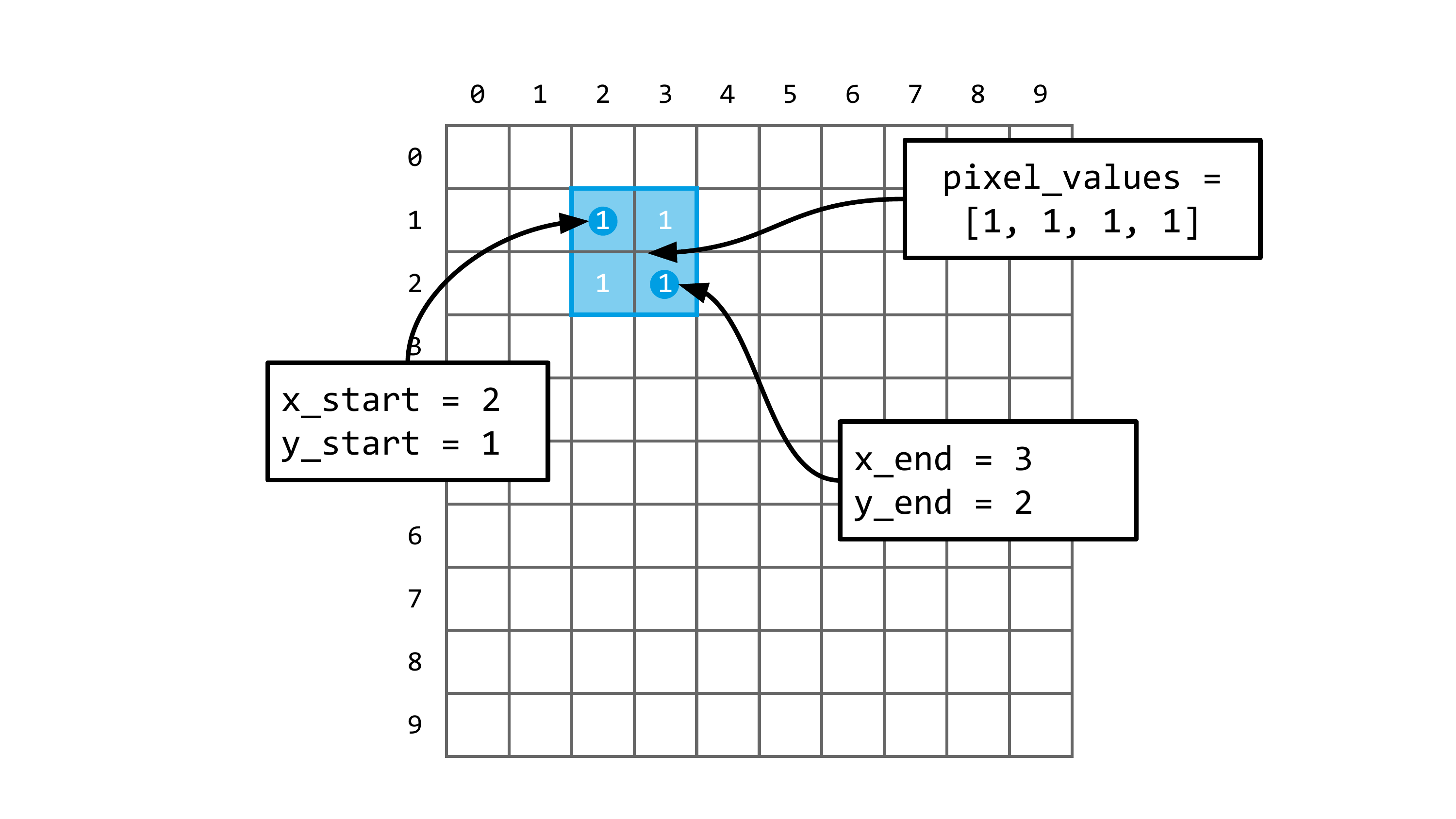
Um ein 2×2-Quadrat zu zeichnen, setzen wir die Koordinaten des oberen linken Punkts auf (62, 30) und die Koordinaten des unteren rechten Punkts auf (63, 31). Die Liste der Werte für die Pixel in dieser Fläche muss 4 Werte enthalten, alle auf 1 gesetzt:

oled.write_pixels(62, 30, 63, 31, [1, 1, 1, 1])

Genau genommen ist die Liste eine flache Struktur, sie wird aber als 2×2-Matrix interpretiert. Die Bitmap sieht also so aus:

1 1
1 1

Abbildung 4.6 zeigt das Konzept der Bitmap für unser 2×2-Quadrat.

Was ist, wenn wir das Quadrat auf 3×3 vergrößern wollen? Dann ändern wir den unteren rechten Punkt auf (64, 32) oder alternativ den oberen linken Punkt auf (61, 29). Die Liste der Werte erweitern wir auf 9 Einträge:

oled.write_pixels(61, 29, 63, 31, [1] * 9)

Die Python-Syntax [1] * 9 erzeugt eine Liste mit 9 Einsen. Das ist eine praktische Abkürzung, um lange Listen mit gleichen Werten zu erstellen.

Die Länge der Liste pixel_values muss immer genau der Anzahl der Pixel in der Fläche entsprechen. Die Werte werden zeilenweise von links nach rechts und von oben nach unten gelesen und auf das Display projiziert.

4.3.2 Ein Kreuz als Bitmap

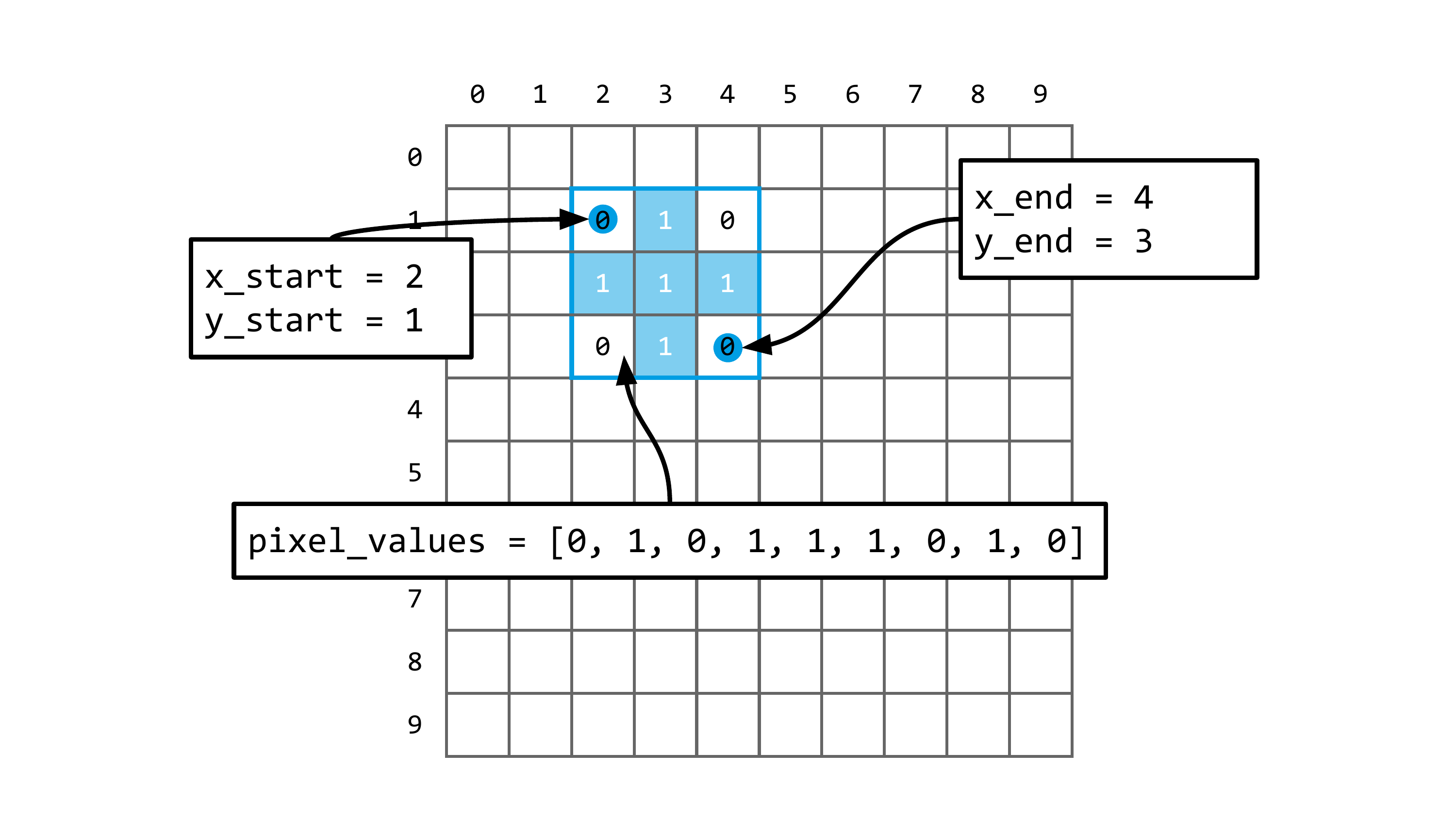
In Abbildung 4.7 sehen wir ein weiteres Beispiel, diesmal für eine Bitmap mit 3×3 Pixeln. Es leuchten nur die Pixel, die ein Kreuzmuster ergeben. Als Liste sieht das so aus:

[0, 1, 0, 1, 1, 1, 0, 1, 0]

Als Matrix dargestellt:

0 1 0
1 1 1
0 1 0

Wenn wir dieses Kreuz öfter zeichnen wollen, speichern wir die Liste der Pixelwerte am besten in einer Variablen:

cross_bitmap = [
    0, 1, 0,
    1, 1, 1,
    0, 1, 0
]

Jetzt können wir das Kreuz einfach zeichnen, indem wir die Variable cross_bitmap an write_pixels() übergeben:

oled.write_pixels(0, 0, 2, 2, cross_bitmap)

Da wir das Quadrat (0, 0) bis (2, 2) angegeben haben, erscheint das Kreuz in der linken oberen Ecke. Wir können die x- und y-Koordinaten anpassen, um das Kreuz an einer anderen Position zu zeichnen, z.B. direkt daneben noch eins, mit einem Pixel Abstand:

oled.write_pixels(0, 0, 2, 2, cross_bitmap)
oled.write_pixels(4, 0, 6, 2, cross_bitmap)

4.3.3 Viele Kreuze mit Schleifen

Was, wenn wir Kreuze über das gesamte Display zeichnen wollen? Ein Kreuz inklusive Abstand benötigt 4 Pixel in der Breite (3 Pixel für das Kreuz, 1 Pixel Abstand). Mit 128 Pixeln in der Breite können wir 32 solcher Blöcke nebeneinander unterbringen.

Anstatt jede Position per Hand zu kodieren, nutzen wir eine Schleife:

for x in range(0, 128, 4):
    oled.write_pixels(x, 0, x + 2, 2, cross_bitmap)

Erinnert euch: Die range()-Funktion erzeugt eine Folge von Zahlen. In diesem Fall starten wir bei 0, enden vor 128 und erhöhen die Zahl in jedem Schritt um 4. Dadurch erhalten wir die x-Koordinaten 0, 4, 8, …, 124. In jedem Schleifendurchlauf zeichnen wir ein Kreuz an der aktuellen x-Position.

Wollen wir das gesamte Display mit Kreuzen füllen, verschachteln wir zwei Schleifen – eine für die Zeilen (y), eine für die Spalten (x):

for y in range(0, 64, 4):
    for x in range(0, 128, 4):
        oled.write_pixels(x, y, x + 2, y + 2, cross_bitmap)

Wenn ihr den Code ausführt, könnt ihr dem Display beim Zeichnen zuschauen. Es füllt sich nach und nach mit Kreuzen, bis das gesamte Display bedeckt ist.

Wir haben damit alle Bausteine beisammen, um nicht nur geometrische Formen, sondern auch komplexere Symbole wie Buchstaben zu zeichnen.

4.4 Buchstaben

Auch Buchstaben auf dem Bildschirm sind nichts anderes als Pixelmuster. Wie bereits erwähnt, ist ein Buchstabe auf dem Tinkerforge-Display 5 Pixel breit und 8 Pixel hoch. Das bedeutet, dass wir für jeden Buchstaben eine Bitmap mit 40 Werten benötigen.

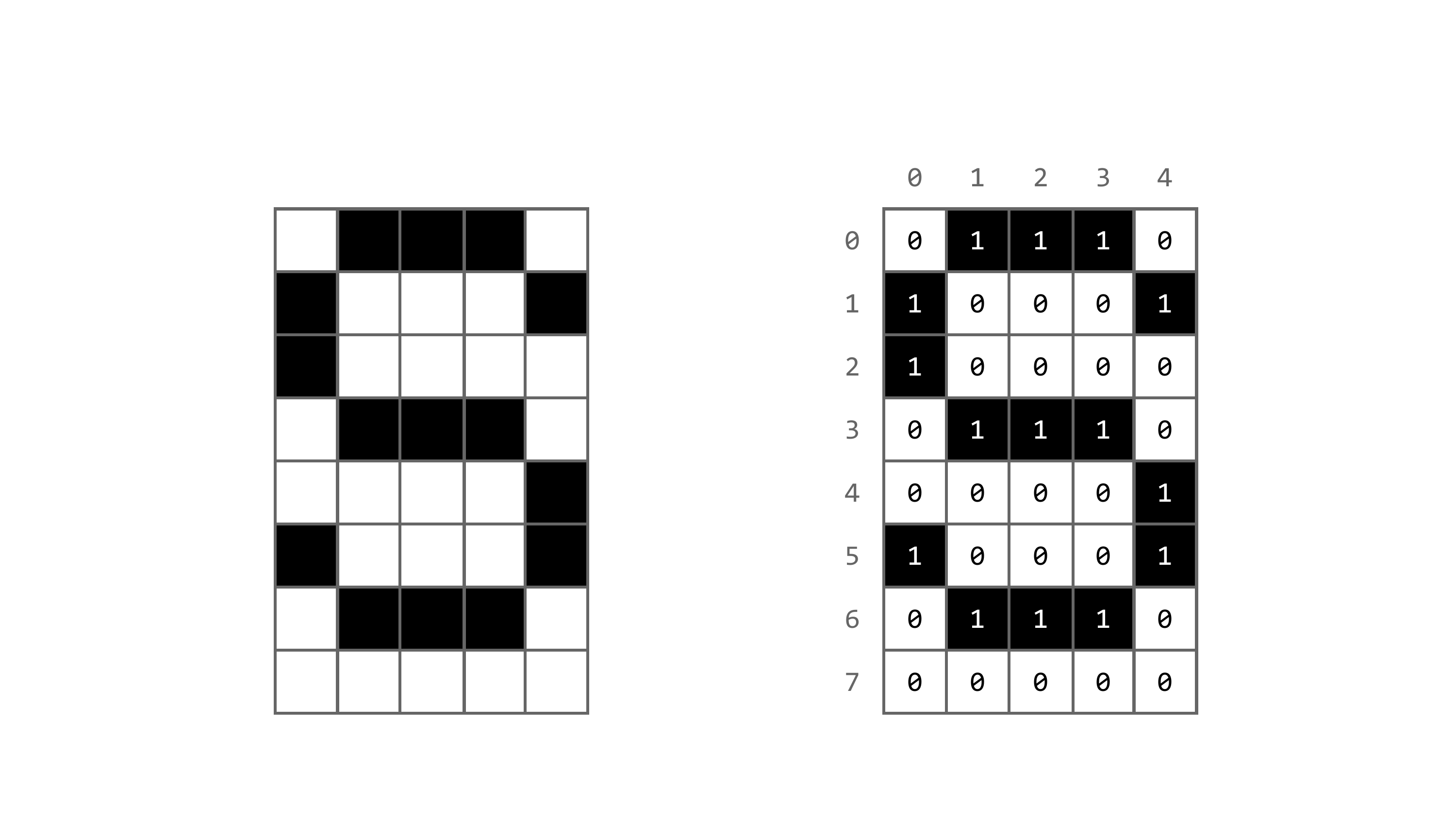
Tinkerforge stellt eine Übersicht der unterstützten Zeichen und deren Pixelmuster auf seiner Webseite bereit. Daraus habe ich den Buchstaben “A” als Bitmap in eine einfache Tabelle übertragen und Pixel, die an sind, schwarz eingefärbt. Das Ergebnis seht ihr in Abbildung 4.8.

Anhand dieser Darstellung können wir die Liste mit Einsen und Nullen ableiten, die wir benötigen, um das “A” auf dem Display darzustellen:

letter_a_bitmap = [
    0, 0, 1, 0, 0,
    0, 1, 0, 1, 0,
    1, 0, 0, 0, 1,
    1, 0, 0, 0, 1,
    1, 1, 1, 1, 1,
    1, 0, 0, 0, 1,
    1, 0, 0, 0, 1,
    0, 0, 0, 0, 0
]

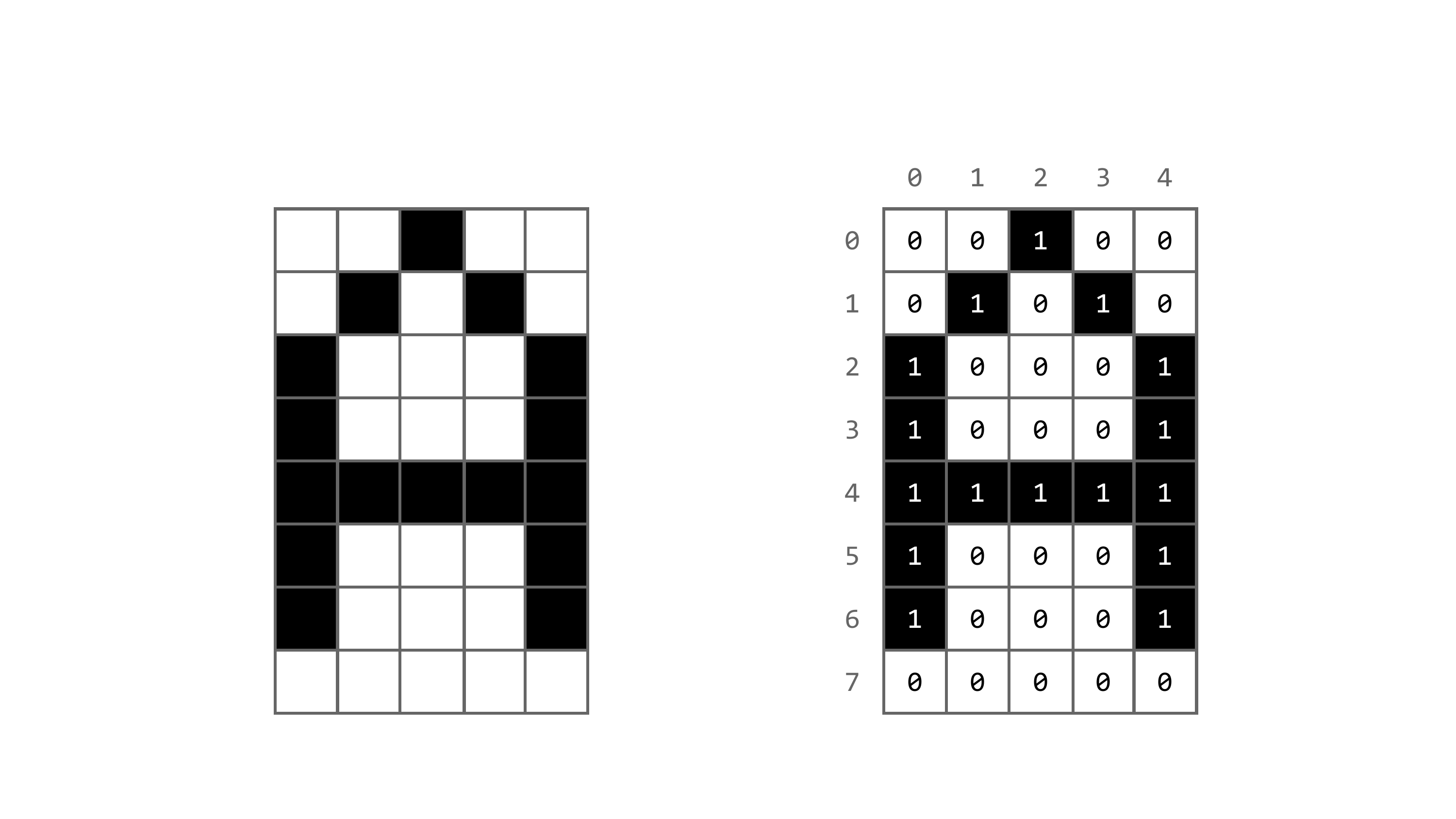
In der Matrixdarstellung erkennt man das “A” recht gut. Jetzt ein Rätsel: Welcher Buchstabe verbirgt sich in der folgenden Bitmap?

letter_unknown_bitmap = [
    0, 1, 1, 1, 0,
    1, 0, 0, 0, 1,
    1, 0, 0, 0, 0,
    0, 1, 1, 1, 0,
    0, 0, 0, 0, 1,
    1, 0, 0, 0, 1,
    0, 1, 1, 1, 0,
    0, 0, 0, 0, 0
]

Zeichnen wir den Buchstaben auf dem Display, um es herauszufinden. Wir kennen die Dimensionen (5×8 Pixel), haben die Bitmap als Liste und müssen nur noch die Position bestimmen. Ich habe mich für die Position (6, 10) als oberen linken Punkt entschieden:

oled.write_pixels(6, 10, 10, 17, letter_unknown_bitmap)

Und? Seht ihr auch ein großes “S”?

Versuchen wir, davor noch das “A” zu schreiben:

oled.write_pixels(1, 10, 5, 17, letter_a_bitmap)

Wir haben richtig gerechnet: Das “A” soll vor dem “S” stehen, also müssen wir mit der x-Koordinate 5 Pixel nach links gehen. Lasst uns noch ein Pixel Platz zwischen beiden Buchstaben lassen. Dann setzen wir die x-Koordinate des “A” auf 0 und die des rechten unteren Punkts auf 4:

oled.write_pixels(0, 10, 4, 17, letter_a_bitmap)

Und nun noch ein “S” ans Ende, damit wir ein sinnvolles Wort schreiben:

oled.write_pixels(0, 10, 4, 17, letter_a_bitmap)
oled.write_pixels(6, 10, 10, 17, letter_unknown_bitmap)
oled.write_pixels(12, 10, 16, 17, letter_unknown_bitmap)

Entscheidet selbst, ob ihr bei dem geschriebenen Wort an eine Spielkarte, den Namen eines Schmerzmittels oder das englische Schimpfwort denkt. Technisch haben wir schlicht drei Buchstaben als Bitmaps auf dem Display dargestellt. Und das ganz ohne die Textfunktion des Displays zu verwenden.

Zur Erinnerung: Das wäre auch viel einfacher gegangen, nur weniger lehrreich:

oled.write_line(0, 0, "Ass")

Wenn ihr beides hintereinander ausführt, steht oben “Ass” per Textfunktion und darunter “ASS” als eigene Bitmaps. Die write_line()-Funktion verwendet intern eine eingebaute Schriftart: Für jedes Zeichen ist in einer Tabelle hinterlegt, welche Pixel im 5×8-Raster leuchten.

Schriftarten für Pixel-Displays sind im Kern nichts anderes als Sammlungen von Bitmaps: Für jedes Zeichen wird festgelegt, welche Pixel leuchten. Wenn ihr eine andere Schrift wollt, erstellt ihr einfach eine neue Bitmap-Tabelle, etwa eine fette oder schmale Variante, und verwendet diese beim Zeichnen.

Diese Bitmap-Schriften funktionieren hervorragend in festen Rastergrößen, stoßen aber an Grenzen, sobald die Größe der Buchstaben beliebig geändert werden soll. Beim Vergrößern treten dann unschöne Treppeneffekte auf. Hier kommen Vektorgrafiken ins Spiel.

4.5 Vektorgrafiken

Während Bitmaps jedes Pixel explizit speichern, beschreiben Vektorgrafiken Objekte über geometrische Formen, etwa “eine Linie von A nach B” oder “ein Kreis mit Mittelpunkt M und Radius r”.

Eine Vektor-Schriftart (wie TrueType) enthält keine 5×8-Raster pro Zeichen, sondern Pfade für die Konturen von “A”, “S” etc. Der Vorteil: Diese Formen lassen sich beliebig vergrößern oder verkleinern, ohne dass Treppeneffekte entstehen. Das ist ideal für hochauflösende Displays und Druck.

Schaut euch zur Verdeutlichung der Problematik einmal die beiden “a” aus Abbildung 4.10 an. Das linke “a” ist eine TrueType-Schriftart, die als Vektorgrafik beschrieben wird. Das rechte “a” ist über eine Bitmap definiert und wurde stark vergrößert. Während das rechte “a” pixelig wirkt – wir sprechen vom Treppeneffekt – ist die als Vektorgrafik beschriebene Variante gestochen scharf, auch in großen Größen.

Abbildung 4.10: Das linke “a” ist eine TrueType-Schriftart, das rechte “a” eine Bitmap. Quelle: Wikipedia.

Wie funktioniert das? Dazu betrachten wir ein anderes Beispiel für eine Vektorgrafik im weit verbreiteten Format Scalable Vector Graphics (SVG). Kopiert den folgenden Code in eine Textdatei und benennt sie vector_graphics.svg. Öffnet die Datei anschließend in einem Webbrowser.

<svg width="440" height="220" xmlns="http://www.w3.org/2000/svg">
  <circle cx="60" cy="60" r="50" stroke="#0085C7" stroke-width="10" fill="none" />
  <circle cx="180" cy="60" r="50" stroke="#000000" stroke-width="10" fill="none" />
  <circle cx="300" cy="60" r="50" stroke="#DF0024" stroke-width="10" fill="none" />
  <circle cx="120" cy="110" r="50" stroke="#FFD500" stroke-width="10" fill="none" />
  <circle cx="240" cy="110" r="50" stroke="#009F3D" stroke-width="10" fill="none" />
</svg>

Ihr solltet ein Bild wie in Abbildung 4.11 sehen. Zoomt nun einmal stark hinein (Strg + Plus bzw. Cmd + Plus). Die Kreise bleiben scharf, ohne Treppeneffekte. Das liegt daran, dass Vektorgrafiken mathematisch beschrieben werden und nicht auf eine feste Pixelauflösung angewiesen sind.

Aber Moment: Wenn Vektorgrafiken auf einem Bildschirm angezeigt werden, müssen sie dann nicht auch als Pixel dargestellt werden? Schließlich besteht doch jedes Bild im Endeffekt aus Pixeln.

Genau. Während Vektorgrafiken das, was auf dem Bildschirm erscheinen soll, über geometrische Formen beschreiben, muss das Bild letztlich in eine Bitmap umgewandelt werden, damit es auf dem Bildschirm angezeigt werden kann. Dieser Prozess wird als Rasterisierung bezeichnet.

In Abbildung 4.12 seht ihr die Vektorgrafik von oben, die in eine Bitmap mit niedriger Auflösung (100 × 50 Pixel) umgewandelt wurde. Wenn man dieses Bild stark vergrößert oder auf ein großes Werbeplakat druckt, erkennt man die Treppeneffekte deutlich. Die Auflösung einer Bitmap ist somit entscheidend für die Bildqualität.

Bei Vektorgrafiken spielt die Auflösung dagegen erst bei der Rasterisierung eine Rolle: Wir können für ein 3×2 m Werbeplakat einfach eine entsprechend hochauflösende Bitmap generieren, ohne dass die Qualität leidet, weil die Vektorgrafik immer die gleichen geometrischen Formen beschreibt.

Aufgrund ihrer Eigenschaften werden Vektorgrafiken insbesondere für Logos, Icons und Schriftarten verwendet, die in verschiedenen Größen dargestellt werden müssen. Für komplexe Bilder mit vielen Farben und Details, wie Fotos, sind Bitmaps jedoch besser geeignet, weil eine Beschreibung als reine Geometrie zu aufwendig wäre.

Am Ende landen aber sowohl Bitmaps als auch Vektorgrafiken auf unserem Display immer als dasselbe: als Liste von Bits für die Pixel. Genau diese Perspektive nehmen wir im nächsten Abschnitt ein.

4.6 Von Bits zum Bild

Wir bleiben in diesem Kapitel bei Bitmaps, denn ein Bildschirm kennt nur Pixel. Egal, ob ein Bild ursprünglich eine Vektorgrafik war oder direkt als Bitmap vorliegt: Um es auf unserem Display anzuzeigen, müssen wir es in eine Liste von Pixelwerten umwandeln und mit write_pixels() zeichnen.

Auf unserem OLED reicht eine Liste mit Binärwerten (0 und 1) aus, um jedes Pixel als ein- oder ausgeschaltet zu kennzeichnen. Für farbige Displays (z.B. Smartphone, TV) werden mehrere Bits pro Pixel benötigt. Ihr erinnert euch an den RGB-Farbcode aus Kapitel 1.

4.6.1 Darth Vader als Pixelart

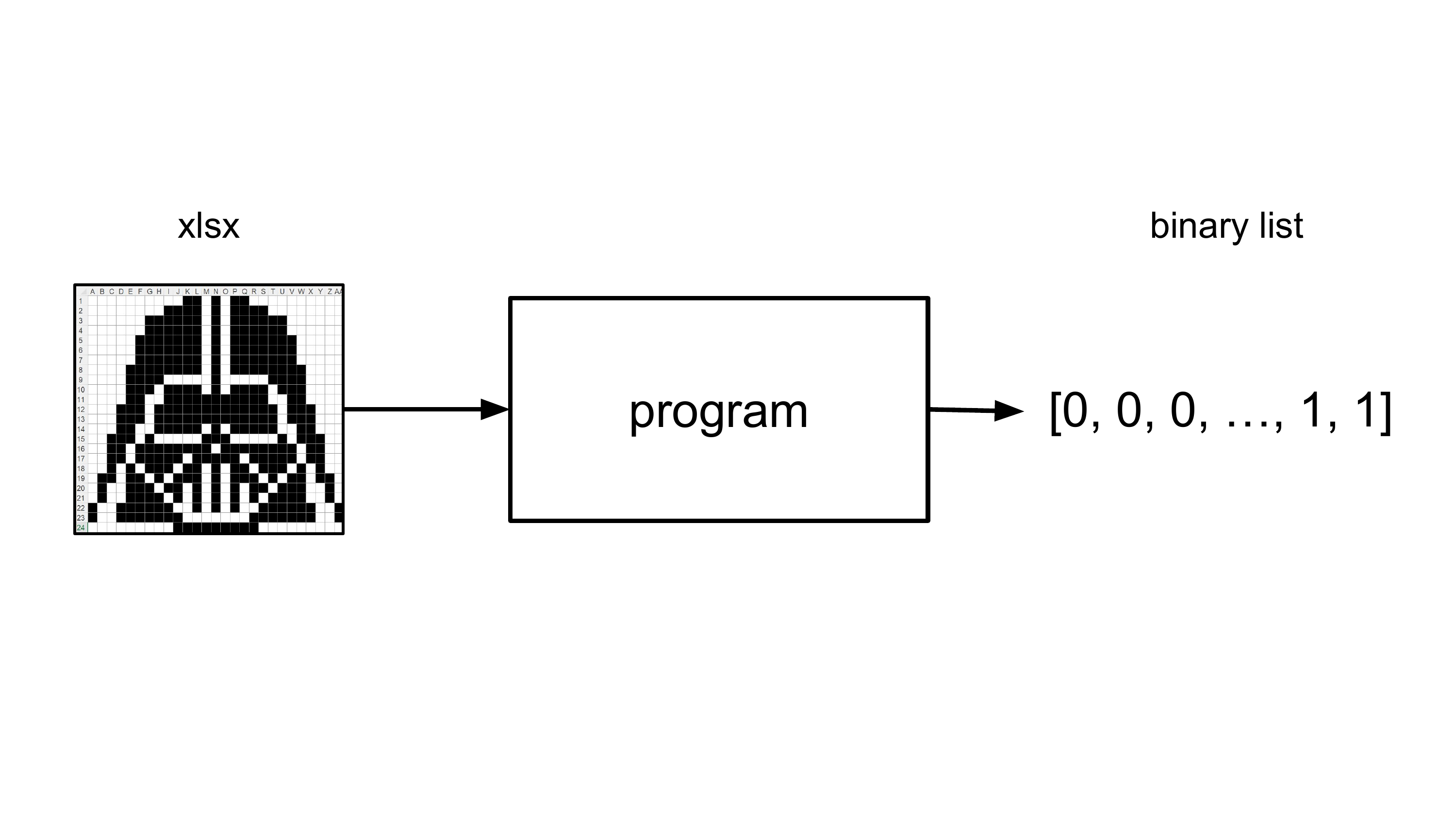
Betrachtet einmal das Bild in Abbildung 4.13. Ihr erkennt bestimmt, was es zeigt: eine Bitmap-Darstellung von Darth Vaders Kopf aus Star Wars. Das Bild ist 27 Pixel breit und 24 Pixel hoch, also insgesamt 648 Pixel. Jedes Pixel ist entweder schwarz oder weiß, das passt problemlos auf unser Display.

Unser Ziel ist es, dieses Bild auf dem Display anzuzeigen. Dafür brauchen wir eine Liste aus Nullen und Einsen, die jedes Pixel repräsentiert. Die Idee, diese Liste per Hand aus einem Bild abzulesen, ist sehr mühsam und fehleranfällig.

Glücklicherweise liegt das Bild bereits digital vor – nicht als Bilddatei, sondern als Excel-Tabelle. Die Idee habe ich aus dem CS50-Kurs der Harvard University übernommen: Dort erstellen Studierende Pixelbilder in Excel, indem sie die Zellen einfärben. Jede Zelle entspricht einem Pixel, das entweder schwarz oder weiß ist.

Die Excel-Datei mit Darth Vaders Maske könnt ihr euch herunterladen und das Ganze selbst ausprobieren.

Wir können das Problem im Sinne des EVA-Modells auffassen: Eingabe sind die Zellfarben in der Excel-Tabelle, Ausgabe soll eine Liste von Bits sein. Dazwischen liegt die Verarbeitung, die wir mit Python programmieren.

4.6.2 Excel mit Python einlesen

Um Excel-Dateien in Python zu lesen, müssen wir das Rad nicht neu erfinden. Es gibt verschiedene Bibliotheken für diesen Job, eine der beliebtesten und einfachsten ist openpyxl. Installiert sie mit:

pip install openpyxl

(MacOS-Nutzer verwenden pip3.)

openpyxl stellt uns die Funktion load_workbook() zur Verfügung, der wir den Pfad der Excel-Datei übergeben können:

from openpyxl import load_workbook
workbook = load_workbook("Darth Vader Pixel Art.xlsx")
1
Wir kündigen an, dass wir die Funktion load_workbook() verwenden möchten.
2
Wir laden die Excel-Datei und speichern das Ergebnis in der Variable workbook.

Ein Excel-Dokument kann mehrere Tabellenblätter enthalten. Wir wählen das Blatt “Darth Vader” aus:

sheet = workbook["Darth Vader"]

4.6.3 Zeile für Zeile die Pixelwerte extrahieren

Um aus der Excel-Darstellung zu einer Liste mit 0 und 1 zu kommen, schreiben wir ein Programm, das genau das Vorgehen simuliert, das wir per Hand machen würden: Zeile für Zeile durch die Tabelle gehen und für jede Zelle von links nach rechts prüfen, ob sie schwarz oder weiß ist.

Für wiederholte Abläufe verwenden wir Schleifen. Die Methode sheet.iter_rows() liefert uns alle Zeilen, über die wir mit einer for-Schleife iterieren können. Jede Zeile ist wiederum eine Liste von Zellen, über die wir ebenfalls iterieren:

for row in sheet.iter_rows():
    for cell in row:
        ...
1
Die äußere Schleife iteriert über jede Zeile im Tabellenblatt.
2
Die innere Schleife iteriert über jede Zelle in der aktuellen Zeile.
3
Hier ergänzen wir gleich den Code, der die Farbe der Zelle prüft.

Was passiert nun in der inneren Schleife? Wir müssen die Farbe der Zelle auslesen. Das geht über die Attribute cell.fill.fgColor.rgb. Die Details muss man nicht auswendig wissen, sie stehen in der Dokumentation.

Probieren wir, die Farbe der Zelle auszulesen und auszugeben:

for row in sheet.iter_rows():
    for cell in row:
        color = getattr(cell.fill.fgColor, "rgb", None)
        print(color)
1
Wir lesen den Farbwert als Hexadezimalzahl aus.
2
Wir geben den Farbwert aus, um zu sehen, wie er aussieht.

Die Ausgabe sieht ungefähr so aus:

00000000
00000000
...
FF000000
FF000000
...

Offenbar bekommen wir 8-stellige Hexadezimalzahlen. Was bedeuten die noch gleich?

4.6.4 Hexadezimale Farbwerte

Im vorigen Kapitel Kapitel 2 haben wir das Binärsystem kennengelernt. Es ist ein Stellenwertsystem zur Basis 2. Ein weiteres, in der Informatik wichtiges System, ist das Hexadezimalsystem zur Basis 16. Es verwendet die Ziffern 0 bis 9 und anschließend die Buchstaben A bis F für die Werte 10 bis 15.

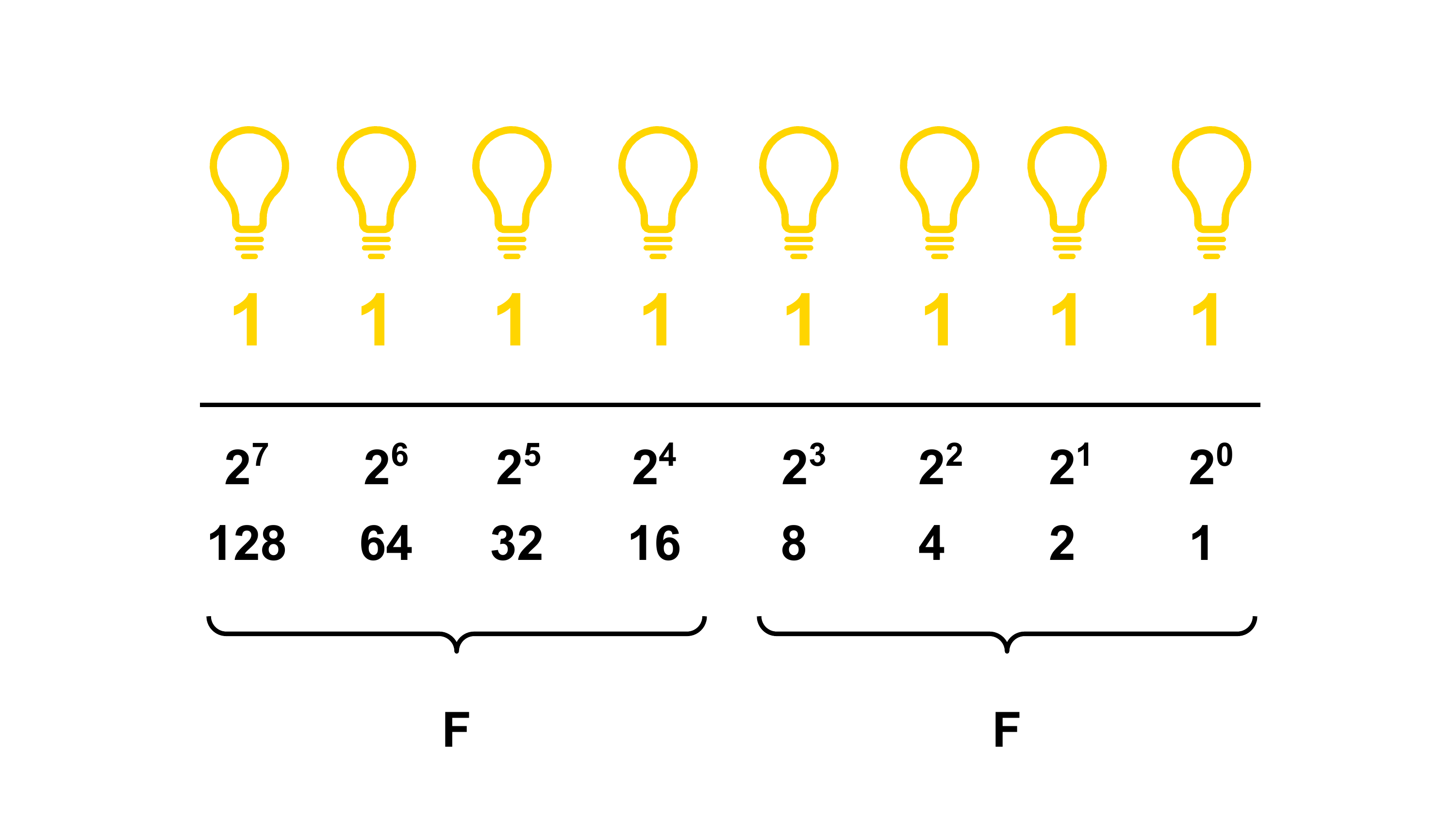
Hexadezimale Zahlen werden häufig verwendet, um Bytes kompakt darzustellen. Wie ihr gleich sehen werdet, passt ein Byte nämlich perfekt in zwei Hexadezimalziffern.

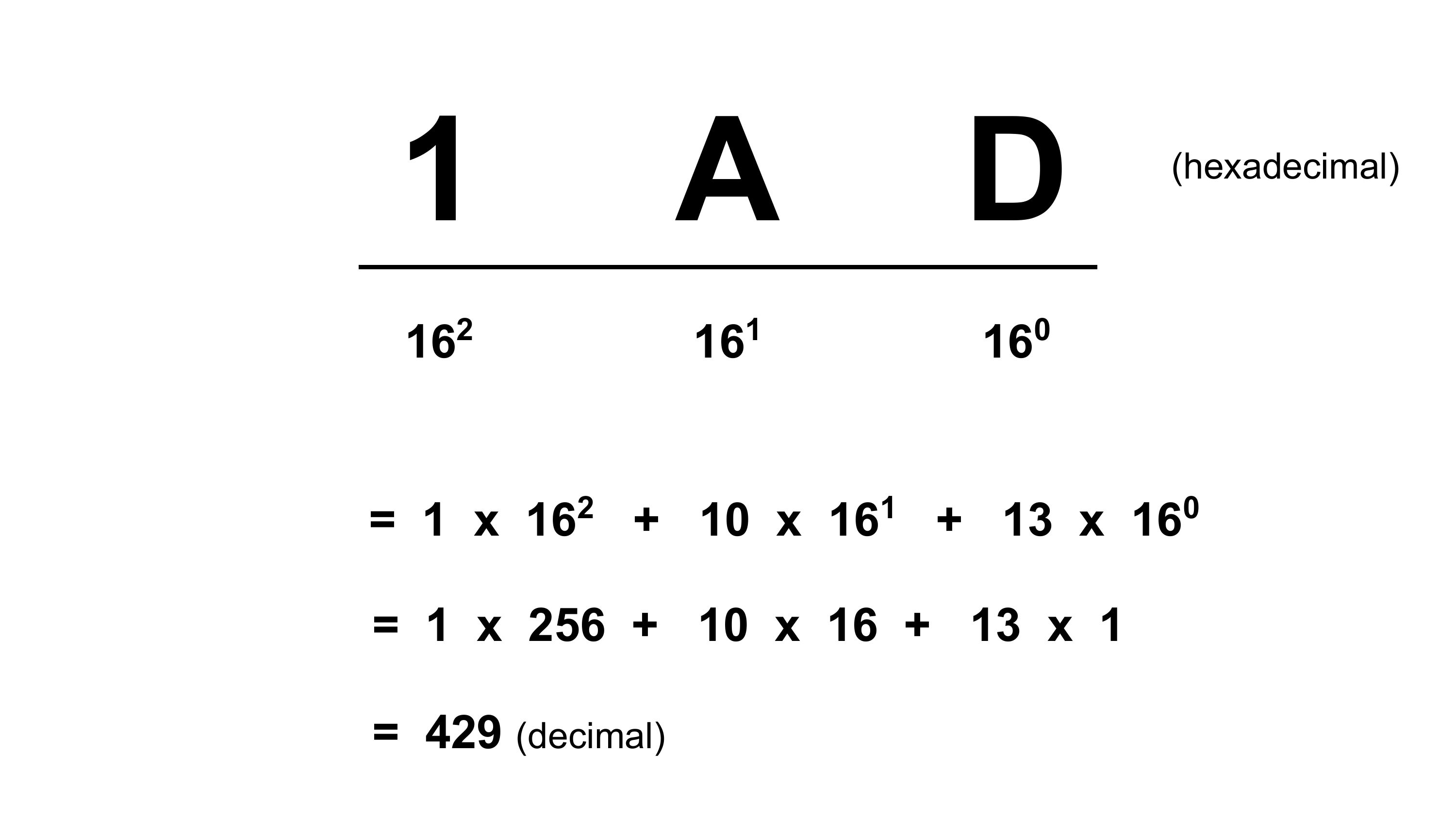
Wir können unser bekanntes Stellenwertschema auf die Basis 16 anwenden:

Die rechte Stelle hat den Wert \(16^0 = 1\), die nächste links den Wert \(16^1 = 16\), dann \(16^2 = 256\) usw. Um den Wert einer Hexadezimalzahl zu berechnen, multiplizieren wir jede Ziffer mit ihrer Stellenwertigkeit und addieren die Ergebnisse.

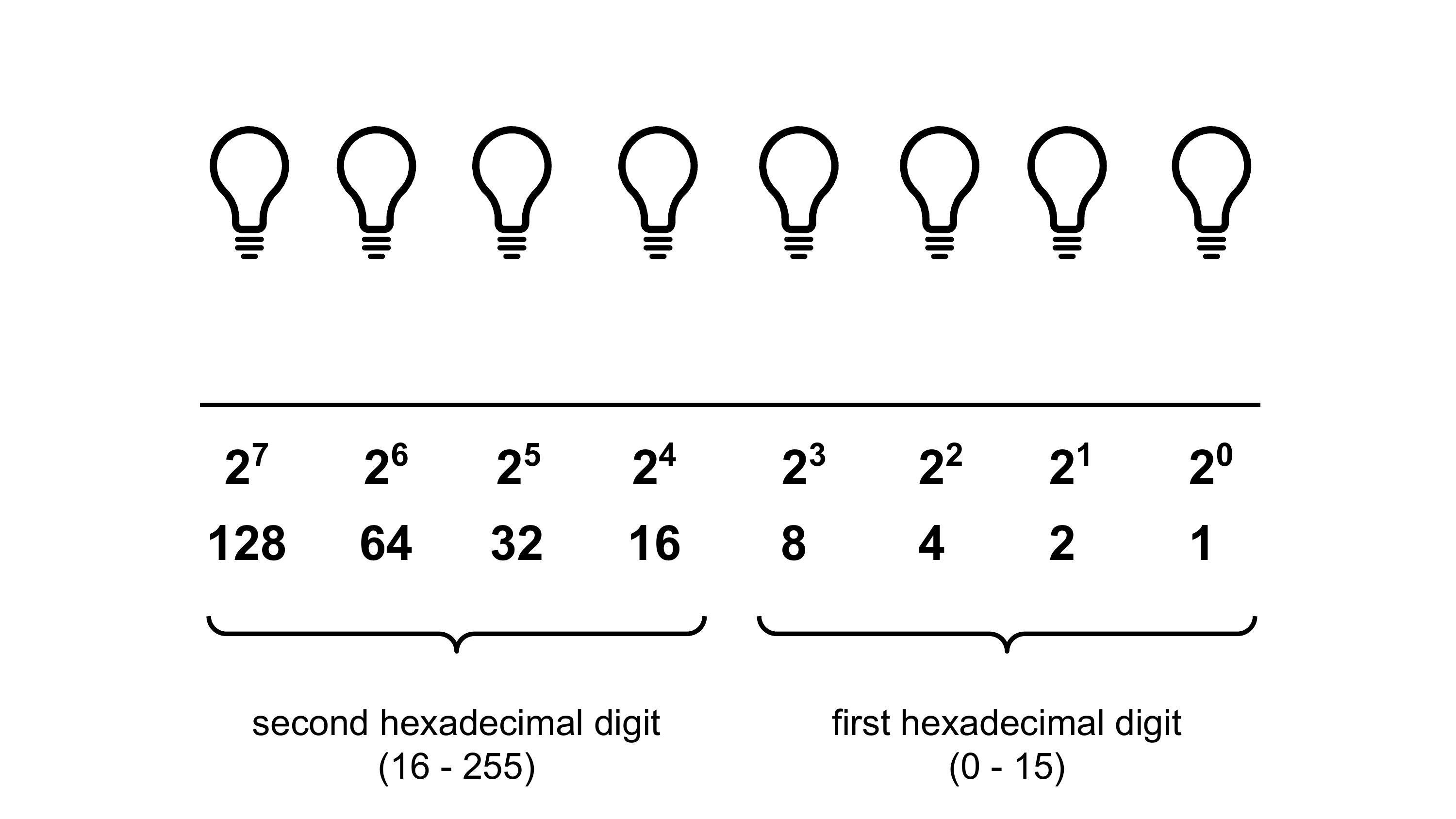
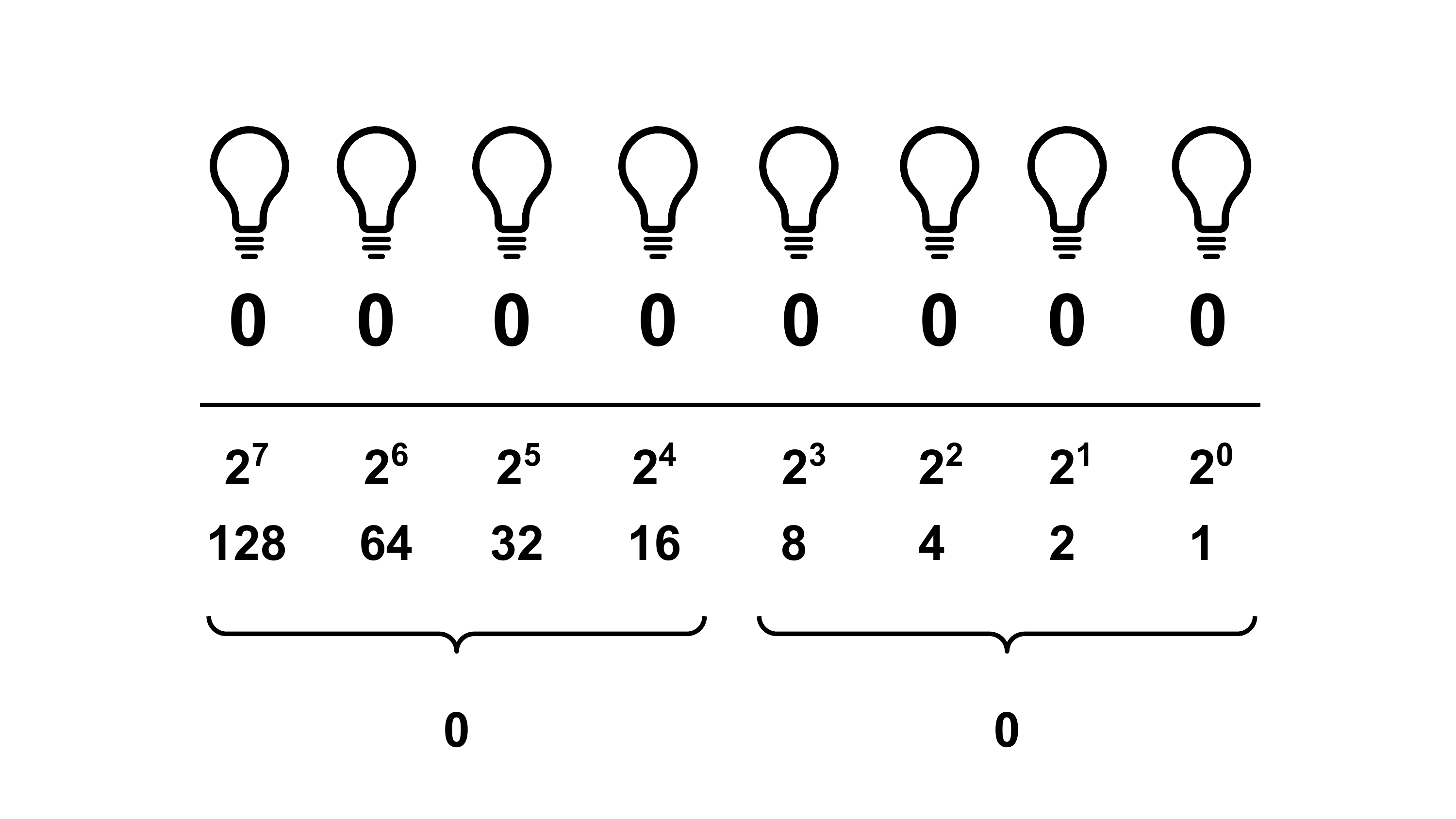
Warum ist das interessant? Mit einer Hexadezimalziffer können wir Werte von 0 bis 15 darstellen. Im Binärsystem benötigen wir dafür vier Bits. Vier Bits entsprechen genau einem halben Byte, einem so genannten Nibble. Zwei Hexadezimalziffern können also alle 256 möglichen Werte eines Bytes (0–255) darstellen.

Abbildung 4.17: Darstellung von Bytes als Hexadezimalzahlen.

Kleine Randnotiz: In der Informatik wird eine Hexadezimalzahl häufig mit einem vorangestellten 0x gekennzeichnet, um klarzumachen, dass es sich um eine Hexadezimalzahl handelt. So wird aus der Zahl 255 im Dezimalsystem die Zahl 0xFF im Hexadezimalsystem.

Alpha-Werte

Zurück zur Ausgabe von oben: Wir haben 8-stellige Hexadezimalzahlen gesehen, obwohl ein RGB-Wert aus drei Bytes (also 6 Hexziffern) besteht. Die Erklärung: Die ersten beiden Ziffern repräsentieren die Transparenz (Alpha-Kanal), gefolgt von den sechs Ziffern für Rot, Grün und Blau.

In unserem Fall sind die Farben entweder komplett schwarz (FF000000) oder komplett weiß (FF000000 für schwarz mit vollem Alpha, später FFFFFFFF für weiß). Die ersten beiden Ziffern FF stehen dabei für den Alpha-Wert: vollständig sichtbar.

Macht einmal den Test und färbt die obere linke Zelle in Rot ein. Nach einem erneuten Lauf (Excel speichern und schließen!) erhaltet ihr z.B.:

FFFF0000
00000000
...

FFFF0000 steht für: FF (Alpha, voll sichtbar), FF (Rot, volle Intensität), 00 (Grün, 0), 00 (Blau, 0) – also Rot.

4.6.5 Die Liste mit Bits erstellen

Jetzt, da wir die Farbwerte verstehen, können wir sie auswerten. Für Darth Vader ist jede schwarze Zelle ein gesetztes Pixel (1), jede nicht-schwarze Zelle ein ausgeschaltetes Pixel (0):

from openpyxl import load_workbook

workbook = load_workbook("Darth Vader Pixel Art.xlsx")
sheet = workbook["Darth Vader"]

bits = []
for row in sheet.iter_rows():
    for cell in row:
        color = getattr(cell.fill.fgColor, "rgb", None)
        if color == "FF000000":        # schwarz
            bits.append(1)
        else:                           # alles andere behandeln wir als weiß
            bits.append(0)

print(f"Bitmap with {len(bits)} bits: {bits}")

Die if-Anweisung entscheidet, ob wir eine 1 oder 0 anhängen. Das Hinzufügen am Ende der Liste erledigt die append()-Methode. Am Ende haben wir eine Liste mit 648 Einträgen, genau so viele wie das Bild Pixel hat.

4.6.6 Anzeige auf dem Display

Wie wir Pixel auf dem Display anzeigen, haben wir in Abschnitt 4.2 gelernt. Jetzt nutzen wir dieselbe write_pixels()-Funktion, um Darth Vaders Maske darzustellen.

Wir müssen nur die Position und Größe des Bildes festlegen. Ich habe mich für die Position (50, 20) als oberen linken Punkt entschieden, so erscheint das Bild ungefähr in der Mitte. Das Bild ist 27 Pixel breit und 24 Pixel hoch, der untere rechte Punkt ist also (76, 43):

oled.write_pixels(50, 20, 76, 43, bits)

Natürlich müssen wir zuvor wie gewohnt den Boilerplate-Code zum Initialisieren des Displays ergänzen. Das komplette Programm sieht dann so aus:

Code 
from openpyxl import load_workbook
from tinkerforge.ip_connection import IPConnection
from tinkerforge.bricklet_oled_128x64_v2 import BrickletOLED128x64V2

ipcon = IPConnection()
ipcon.connect('localhost', 4223)
oled = BrickletOLED128x64V2('25zo', ipcon)
oled.clear_display()

workbook = load_workbook("xlsx/Darth Vader Pixel Art.xlsx")
sheet = workbook["Darth Vader"]

bits = []
for row in sheet.iter_rows():
    for cell in row:
        color = getattr(cell.fill.fgColor, "rgb", None)
        if color == "FF000000":
            bits.append(1)
        else:
            bits.append(0)

print(f"Bitmap with {len(bits)} bits: {bits}")
oled.write_pixels(50, 20, 76, 43, bits)

Und voilà: Darth Vader erscheint auf dem Display!

4.6.7 Eine Bitmap speichern

Wir haben ein Programm geschrieben, das eine Bitmap aus Excel ausliest und auf dem Display anzeigt. Excel ist dafür aber eher eine Notlösung. Für Bitmaps gibt es besser geeignete Formate, z.B. BMP (Bitmap). Es ist ein einfaches, unkomprimiertes Format, das die Pixelwerte direkt als Abfolge von Bits speichert.

Wenn wir das händisch machen wollten, müssten wir uns mit dem genauen Aufbau des BMP-Formats beschäftigen. Das besteht neben den Farbwerten nämlich auch aus einem so genannten Header, der Metainformationen wie Breite, Höhe oder die Farbtiefe eines Bildes speichert. Das sparen wir uns an dieser Stelle und nutzen stattdessen wieder eine Bibliothek, die alle einfacher macht: Pillow.

Installiert sie mit:

pip install Pillow

(MacOS-Nutzer: pip3.)

Mit Pillow können wir Bilder bequem erstellen und speichern. Für Darth Vader (27×24 Pixel, Schwarzweiß) sieht das so aus:

from PIL import Image
...
image = Image.new('1', (27, 24))
image.putdata(bits)
image.save("xlsx/darth_vader.bmp")
1
Wir importieren die Image-Klasse aus PIL (Teil von Pillow).
2
Wir erstellen ein neues Bildobjekt mit der Größe 27×24 Pixel im Modus "1" (Schwarzweiß).
3
Wir setzen die Pixelwerte des Bildes mit unserer Liste bits (zeilenweise von links nach rechts, oben nach unten).
4
Wir speichern das Bild als BMP-Datei.

Zuerst erstellen wir eine leere Hülle für unsere Bild und geben die Dimensionen sowie die Farbtiefe an. Anschließend übergeben wir dem Bild die Daten, hier unsere Liste bits mit den Nullen und Einsen. Mit image.save() speichern wir die Bitmap-Datei ab. Im Ordner xlsx solltet ihr nun die Datei darth_vader.bmp finden.

Abbildung 4.19: Darth Vader als Bitmap-Datei auf eurer Festplatte.

Damit haben wir die Kette geschlossen: Excel-Pixel → Bitliste → Anzeige auf dem Display → echte Bitmap-Datei. Im nächsten Schritt erweitern wir das Ganze auf Farbbilder.

4.7 Farbe

Bisher haben wir nur Schwarzweiß-Bitmaps verwendet, in denen ein Pixel entweder 0 (schwarz) oder 1 (weiß) ist. Für unser Display reicht das, aber typische Bildschirme arbeiten mit Farben.

Die wichtigste Grundlage dafür, nämlich den RGB-Code, haben wir bereits in Kapitel 1 kennengelernt.

4.7.1 Bitmaps im RGB-Format

In Abbildung 4.20 seht ihr eine farbige Bitmap von Super Mario, wie sie auf der 8-Bit-Konsole Nintendo Entertainment System (NES) über den Bildschirm geflimmert ist. Die Auflösung der NES-Konsole war 256 × 240 Pixel – deutlich weniger als heutige Full-HD-Bildschirme, aber für viel Spielspaß ausreichend.

Super Mario in dieser Darstellung ist 16 Pixel breit und 16 Pixel hoch, also 256 Pixel. Jedes Pixel ist farbig und wird durch einen RGB-Wert (3 Bytes) repräsentiert. Damit benötigt die gesamte Bitmap 256 Pixel × 3 Bytes = 768 Bytes Speicherplatz. Übrigens: Die NES-Spielekonsole konnte nur 256 Farben gleichzeitig darstellen, was 8 Bits pro Pixel entspricht. In diesem Fall wären es 256 Pixel × 1 Byte = 256 Bytes. Heute sind 24 Bits (3 Bytes) pro Pixel üblich, was 16,7 Millionen Farben ermöglicht.

Zum Vergleich: Darth Vader hatte 27×24 = 648 Pixel, aber nur 1 Bit pro Pixel. Das sind 648 Bits = 81 Bytes. Ein größeres Bild kann also weniger Speicher benötigen, wenn es nur Schwarzweiß ist. Die Farbtiefe spielt neben der Auflösung eine entscheidende Rolle für die Dateigröße.

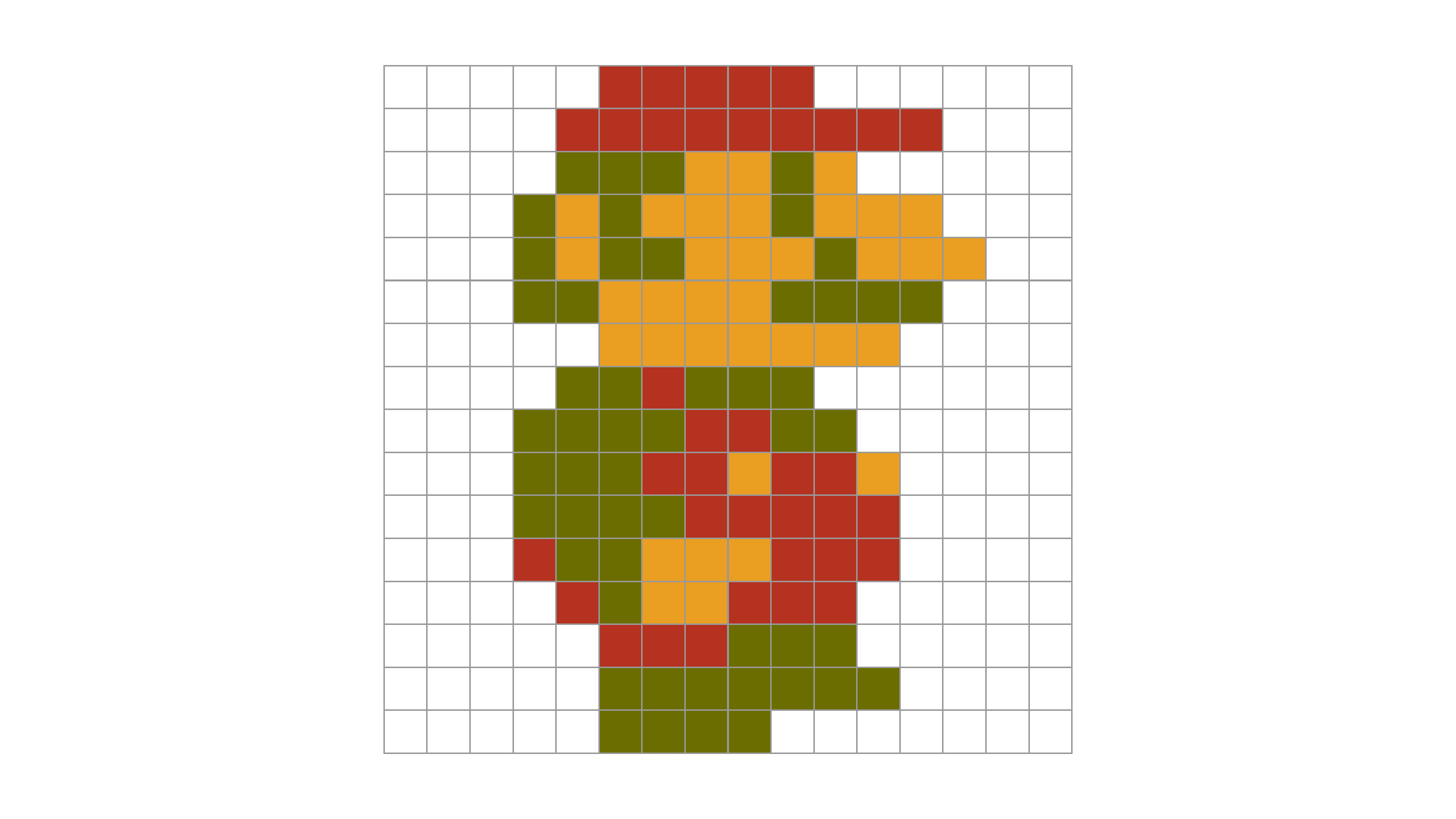
Auch Super Mario habe ich als Excel-Tabelle erstellt, genau wie Darth Vader. Ihr könnt die Datei hier herunterladen.

Wir können unser Programm von oben grundsätzlich wiederverwenden, müssen es aber anpassen: Statt 0 oder 1 pro Pixel wollen wir die RGB-Werte in eine Liste von Dreiertupeln überführen: Ein Wert für jeden Farbkanal im RGB-Code.

Wir laden zunächst die neue Excel-Datei und das Tabellenblatt:

workbook = load_workbook("Super Mario Pixel Art.xlsx")
sheet = workbook["Super Mario"]

Die verschachtelten Schleifen bleiben, aber diesmal interessieren uns nicht nur Schwarz und Weiß, sondern die vollen RGB-Farben. openpyxl liefert die Farbwerte wieder als 8-stellige Hexadezimalzahlen (inklusive Alpha-Kanal). Uns interessieren nur die letzten 6 Ziffern:

bitmap = []
for row in sheet.iter_rows():
    for cell in row:
        color = getattr(cell.fill.fgColor, "rgb", None)
        color = color[2:]
        print(color)
1
Wir schneiden die ersten beiden Ziffern (Alpha-Wert) ab.
2
Wir prüfen, ob wir tatsächlich 6-stellige RGB-Werte erhalten.

Die Ausgabe sieht z.B. so aus:

FFFFFF
FFFFFF
...
B53120
B53120
...

Für die Bildspeicherung im RGB-Format benötigt Pillow pro Pixel ein Dreiertupel mit Dezimalwerten, z.B. für drei weiße Pixel:

bitmap = [(255, 255, 255), (255, 255, 255), (255, 255, 255)]

Wir müssen also:

  1. Den Hex-String RRGGBB in seine Bestandteile zerlegen und
  2. Jede Komponente in eine Dezimalzahl umwandeln.

Beides erledigt Python für uns:

...
color = getattr(cell.fill.fgColor, "rgb", None)
color = color[2:]

r = int(color[0:2], 16)
g = int(color[2:4], 16)
b = int(color[4:6], 16)
print(r, g, b)
1
Wir extrahieren die ersten beiden Ziffern (Rot) und wandeln sie in eine Dezimalzahl um.
2
Wir extrahieren die nächsten beiden Ziffern (Grün).
3
Wir extrahieren die letzten beiden Ziffern (Blau).
4
Wir prüfen, ob die Umwandlung funktioniert hat.

Die Ausgabe beginnt z.B. so:

255 255 255
255 255 255
...
181 49 32
...

Nun sammeln wir die RGB-Werte in einer Liste von Tupeln:

bitmap = []
for row in sheet.iter_rows():
    for cell in row:
        color = getattr(cell.fill.fgColor, "rgb", None)
        color = color[2:]
        r = int(color[0:2], 16)
        g = int(color[2:4], 16)
        b = int(color[4:6], 16)
        rgb_tuple = (r, g, b)
        bitmap.append(rgb_tuple)

Mit dieser Liste bitmap können wir nun ein farbiges Bild von Super Mario erzeugen und speichern. Das funktioniert analog zu Darth Vader oben, nur dass wir diesmal den Modus 'RGB' und eine Dimensionierung von 16 × 16 Pixeln verwenden:

image = Image.new('RGB', (16, 16))
image.putdata(bitmap)
image.save("xlsx/super_mario_color.bmp")

Wenn ihr die Datei super_mario_color.bmp öffnet, seht ihr Mario in Farbe.

4.7.2 Struktur einer Bitmap-Datei

Schauen wir uns nun die Dateigröße an. Im Datei-Explorer oder im Terminal könnt ihr euch die Details einer Datei anzeigen lassen. Auf der Kommandozeile in Windows mit dem Befehl dir, unter Mac/Linux geht das mit ls -lh. So ungefähr sieht die Ausgabe aus:

28.10.2025  19:41    822 super_mario_color.bmp

Die Zahl direkt vor dem Dateinamen ist die Dateigröße in Bytes. In meinem Fall sind es 822 Bytes.

Rein rechnerisch bräuchten wir aber nur:

\[16 \cdot 16 \cdot 3 = 768\]

Bytes, denn wir haben 16×16 = 256 Pixel und jedes Pixel benötigt 3 Bytes. Wo kommen also die restlichen 54 Bytes her?

Die Erklärung: Eine Bitmap-Datei (und praktisch jede andere Datei auch) enthält neben den eigentlichen Informationen (hier: Pixelwerte) noch Metainformationen, also Informationen über das Bild. Dazu gehören z.B. Breite, Höhe und Farbtiefe. Diese Metadaten stehen im sogenannten Header am Anfang der Datei.

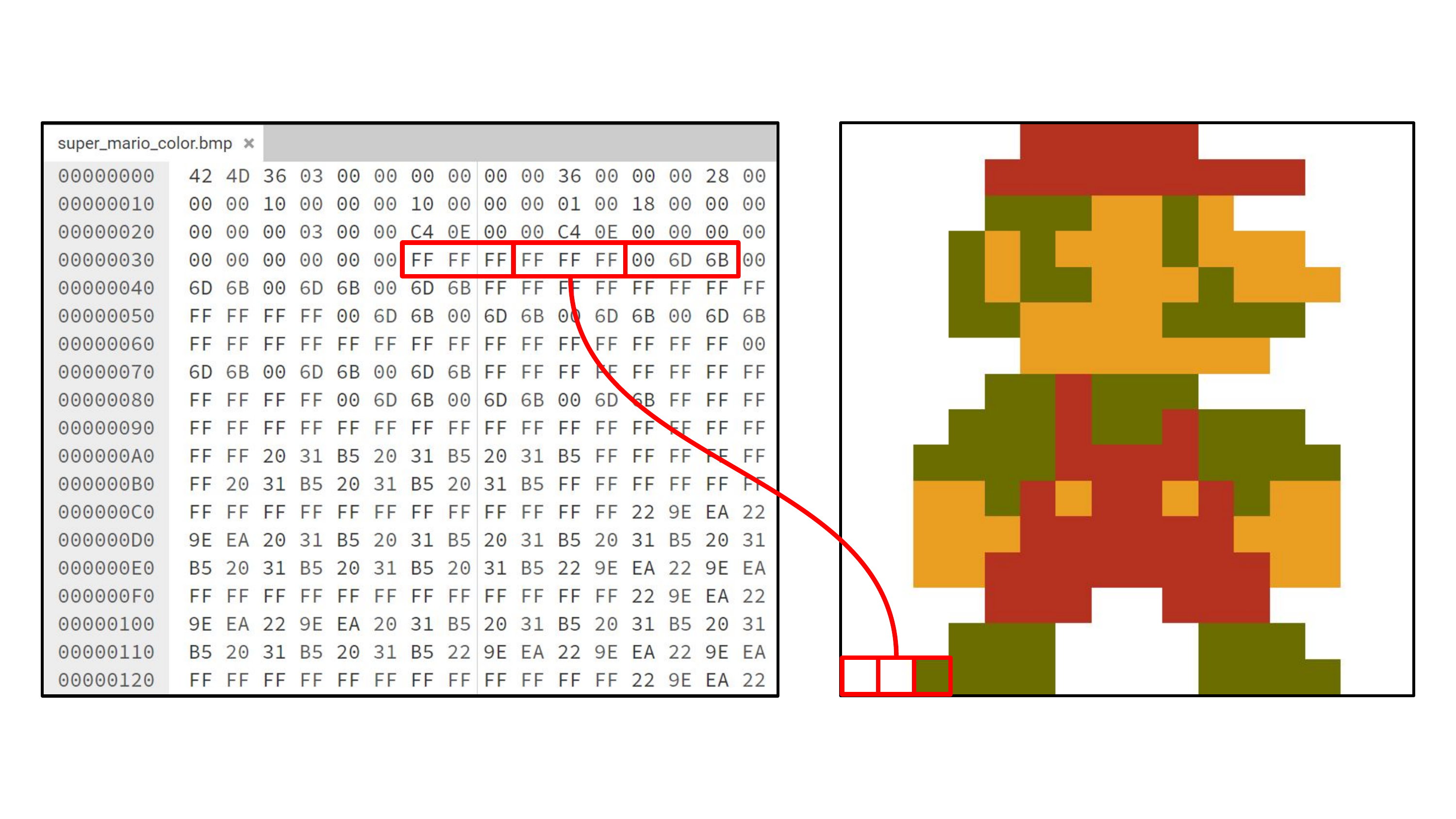
Die wichtigsten Strukturelemente einer Bitmap-Datei sind in Abbildung 4.21 dargestellt. Wir sehen dort die Datei in einem Hexadezimal-Editor. Jedes Kästchen repräsentiert ein Byte (2 Hexadezimalziffern). Die farbigen Bereiche kennzeichnen die verschiedenen Abschnitte der Datei.

  • Der kleine gelbe Bereich am Anfang ist 14 Bytes lang und stellt den Datei-Header dar. Die ersten beiden Bytes 42 und 4D stehen für die ASCII-Zeichen “B” und “M” – ein Kennzeichen für Bitmap-Dateien. Hier steht auch die Gesamtgröße der Datei (z.B. 36 03 00 00, was 822 Bytes entspricht; im sogenannten Little-Endian-Format sind die Bytes in umgekehrter Reihenfolge gespeichert) und die Position, an der die eigentlichen Pixelwerte beginnen (hier: Byte 54).
  • Direkt danach folgt der rosafarbene Bereich mit 40 Bytes: der DIB-Header (Device Independent Bitmap). Hier sind u.a. Breite, Höhe und Farbtiefe gespeichert. Die 18 steht z.B. für 24 Bits Farbtiefe.
  • Erst danach folgen die eigentlichen Pixelwerte (grün markiert). In unserem Fall sind das 768 Bytes.

Probiert es am besten selbst aus: Öffnet die Webseite hexed.it in eurem Browser, ladet super_mario_color.bmp und schaut euch die Datei an. Der Editor zeigt jedes Byte als Hexadezimalzahl an. In Abbildung 4.22 sind die Farbwerte der ersten drei Pixel rot umrandet.

Es passt also alles zusammen:

  • 14 Bytes Datei-Header
  • 40 Bytes DIB-Header
  • 768 Bytes Pixelwerte

Das macht insgesamt 822 Bytes. Wir haben damit ein sehr konkretes Beispiel dafür, wie Bilddaten im Computer gespeichert werden.

Im nächsten Schritt machen wir diese Bilder lebendig.

4.8 Animationen

Viele Anwendungen, z.B. Videospiele wie Super Mario, kommen mit statischen Bildern nicht aus. Mario kann laufen, hüpfen und Feuerkugeln schleudern. Auch bei Videoclips auf YouTube oder Filmen auf Netflix stehen bewegte Bilder im Vordergrund. Wie funktionieren solche bewegten Bilder?

Das Verständnis von statischen Bildern ist die Grundvoraussetzung dafür. Eine Animation besteht im Kern aus einer schnellen Abfolge von Einzelbildern (Frames), die nacheinander angezeigt werden. Wenn die Bilder schnell genug wechseln, entsteht der Eindruck von Bewegung. Unser Gehirn kann ab einer bestimmten Bildwechselrate nicht mehr zwischen einzelnen Bildern unterscheiden.

Um das einmal Hands-On zu erfahren, versuchen wir, Mario zum Laufen zu bringen. Dazu benötigen wir mehrere Bilder, die nacheinander die unterschiedlichen Posen abbilden, die Mario beim Laufen einnimmt. In Abbildung 4.23 seht ihr drei solcher Bilder (die werden auch Sprites genannt) – direkt aus dem Spiel “Super Mario Bros.” der 1980er-Jahre.

Abbildung 4.23: Drei Bilder – oder Frames – um Mario zum Laufen zu bringen.

Ein Sprite ist ein kleines Bild, das in Videospielen Figuren oder Objekte darstellt. In der Regel sind Sprites Teil einer größeren Grafikdatei, des sogenannten Sprite-Sheets. Jedes Bild im Sprite-Sheet repräsentiert eine bestimmte Pose oder Aktion. Indem das Spiel schnell zwischen diesen Bildern wechselt, entsteht der Eindruck von Bewegung.

Das fertige Ergebnis einer Mario-Animation seht ihr in Abbildung 4.24. Es handelt sich um ein GIF (Graphics Interchange Format). Ein GIF ist ein Bildformat, das mehrere Einzelbilder in einer Datei speichern kann. Jedes Einzelbild wird als Frame bezeichnet, und die Frames werden in schneller Abfolge abgespielt.

Wir können dasselbe Prinzip nutzen, um eine Animation auf unser OLED-Display zu bringen: Wir zeigen mehrere Bitmaps nacheinander an und legen dazwischen kurze Pausen ein. Unser Display hat allerdings eine Einschränkung: Es kann nur Schwarzweiß. Also müssen wir unsere farbigen Sprites zunächst in Graustufen und dann in Schwarzweiß umwandeln.

4.9 Transformationen

Der große Vorteil digitaler Bilder ist, dass wir sie mit einfacher Arithmetik fast beliebig bearbeiten können. Viele Fotofilter (z.B. in Instagram oder Snapchat) basieren auf relativ einfachen Berechnungen pro Pixel.

Für unsere Zwecke, ein Bild von Farbe zu Schwarzweiß zu transformieren, brauchen wir zwei Schritte:

  1. Wir transformieren jedes Pixel eines Farbbilds in einen Grauwert (Graustufenbild).
  2. Wir wandeln die Graustufen in Schwarzweiß um, indem wir einen Schwellenwert festlegen.

Wir demonstrieren das wieder an Super Mario.

4.9.1 Graustufen

In Abbildung 4.25 seht ihr ein Farbbild und die entsprechende Graustufenversion.

Um ein Farbbild in ein Graustufenbild zu verwandeln, müssen wir für jedes Pixel einen Helligkeitswert (Luminanz) berechnen. Eine einfache Möglichkeit wäre der Durchschnitt der drei Farbkanäle:

\[ \text{luminance} = \frac{R + G + B}{3} \]

Besser an die menschliche Wahrnehmung angepasst ist jedoch eine gewichtete Summe, denn unser Auge reagiert empfindlicher auf Grün und Rot als auf Blau:

\[ \text{luminance} = 0.299 \cdot R + 0.587 \cdot G + 0.114 \cdot B \]

Wir wollen Mario möglichst menschenähnlich erscheinen lassen und verwenden deshalb diese gewichtete Summe.

In Python sieht die Luminanzberechnung so aus:

luminance = 0.299 * r + 0.587 * g + 0.114 * b
luminance = round(luminance)

round() wandelt den berechneten Wert in eine Ganzzahl um, denn die RGB-Werte müssen schließlich Ganzzahlen sein.

Zuerst laden wir das Farbbild von Mario mit Pillow:

from PIL import Image
image = Image.open("super_mario_color.bmp")
1
Mit Image.open() laden wir die Bitmap-Datei und erhalten ein Bildobjekt.

Sobald wir ein Bild geladen haben, können wir über image.getpixel() den Farbwert eines bestimmten Pixels auslesen. Testen wir das Pixel in der linken oberen Ecke (0, 0):

pixel = image.getpixel((0, 0))
print(pixel)

Die Ausgabe lautet:

(255, 255, 255)

Wir erhalten also ein Tupel mit den RGB-Werten. Extrahieren wir sie und berechnen die Luminanz:

pixel = image.getpixel((0, 0))
r = pixel[0]
g = pixel[1]
b = pixel[2]

luminance = 0.299 * r + 0.587 * g + 0.114 * b
luminance = round(luminance)
print(f"R: {r}, G: {g}, B: {b}, Luminance: {luminance}")

Für das sechste Pixel in der ersten Reihe (x = 5, y = 0) erwarten wir einen rötlichen Wert (Marios Mütze):

pixel = image.getpixel((5, 0))
r = pixel[0]
g = pixel[1]
b = pixel[2]

luminance = 0.299 * r + 0.587 * g + 0.114 * b
luminance = round(luminance)
print(f"R: {r}, G: {g}, B: {b}, Luminance: {luminance}")

Die Ausgabe sieht z.B. so aus:

R: 181, G: 49, B: 32, Luminance: 87

Damit wir die Umrechnung nicht für jedes Pixel neu schreiben müssen, kapseln wir sie in einer Funktion:

def rgb_to_luminance(rgb_tuple):
    r = rgb_tuple[0]
    g = rgb_tuple[1]
    b = rgb_tuple[2]

    luminance = 0.299 * r + 0.587 * g + 0.114 * b
    luminance = round(luminance)
    return luminance
1
Die Funktion rgb_to_luminance erwartet ein Tupel (R, G, B) und gibt die Luminanz als Ganzzahl zurück.

Jetzt können wir für beliebige Pixel einfach:

pixel = image.getpixel((4, 0))
luminance = rgb_to_luminance(pixel)
print(f"Luminance of pixel (4,0): {luminance}")

4.9.2 Bitmap in Graustufen umwandeln

Jetzt müssen wir nur noch die neue Funktion auf alle Pixel anwenden und das Ergebnis speichern. Dazu können wir erneut zwei Schleifen einsetzen, die eine für jede Zeile, die andere für jedes Pixel in einer Zeile. Dafür benötigen wir die Breite und Höhe des Bildes, die wir beide auf einen Schlag mit image.size auslesen können:

w, h = image.size

Nun iterieren wir mit zwei verschachtelten for-Schleifen über alle Pixelkoordinaten und sammeln die Luminanzwerte in einer Liste:

w, h = image.size
grayscale_values = []
for y in range(h):
    for x in range(w):
        r, g, b = image.getpixel((x, y))
        luminance = rgb_to_luminance((r, g, b))
        grayscale_values.append(luminance)

(Vertipper in der Variablenname sind in eurem Code bitte zu vermeiden – hier nennen wir sie besser grayscale_values.)

Mit den gesammelten Graustufenwerten erzeugen wir ein neues Bild:

grayscale_image = Image.new("L", (w, h))  # Modus "L" für Graustufen
grayscale_image.putdata(grayscale_values)
grayscale_image.save("super_mario_grayscale.bmp")

Das Ergebnis seht ihr in Abbildung 4.26.

Der vollständige Code zur Umwandlung von Farbe in Graustufen sieht so aus:

Listing 4.1: Der vollständige Code zur Umwandlung von Farbe in Graustufen.
Code 
from PIL import Image
image = Image.open("xlsx/super_mario_color.bmp")

def rgb_to_luminance(rgb_tuple):
    r = rgb_tuple[0]
    g = rgb_tuple[1]
    b = rgb_tuple[2]

    luminance = 0.299 * r + 0.587 * g + 0.114 * b
    luminance = round(luminance)
    return luminance

w, h = image.size
grayscale_values = []
for y in range(h):
    for x in range(w):
        r, g, b = image.getpixel((x, y))
        luminance = rgb_to_luminance((r, g, b))
        grayscale_values.append(luminance)

print(f"Grayscale bitmap with {len(grayscale_values)} pixel values: {grayscale_values}")

grayscale_image = Image.new("L", (w, h))
grayscale_image.putdata(grayscale_values)
grayscale_image.save("xlsx/super_mario_grayscale.bmp")

4.9.3 Schwarzweiß

Unser Display kann nur zwei Zustände: Pixel an oder aus. Aus dem Graustufenbild müssen wir also im letzten Schritt ein reines Schwarzweißbild erzeugen. Aber wie?

Die Frage ist: Welche Pixel aus dem Graustufenbild sollen im Schwarzweißbild schwarz oder weiß sein? Dazu wäre es sinnvoll, dass wir uns einen Schwellenwert setzen, der die Grenze zwischen schwarz und weiß definiert. Alle dunkleren Graustufenwerte unterhalb des Schwellenwerts werden zu schwarz (0), alle darüber oder gleich dazu zu weiß (1). Wir implementieren das direkt als Funktion:

def luminance_to_bw(luminance, threshold=128):
    if luminance < threshold:
        return 0
    else:
        return 1
1
Die Funktion erwartet einen Luminanzwert und einen optionalen Schwellenwert (Standard: 128) und liefert 0 (schwarz) oder 1 (weiß).

Wie zuvor mit der Graustufenumwandulung können wir die neue Funktion auf jedes Pixel anwenden. Und zwar in der inneren Schleife, damit wir die neue Funktion auf alle Pixel des Graustufenbildes anwenden können:

Code 
from PIL import Image
image = Image.open("xlsx/super_mario_grayscale.bmp")

def luminance_to_bw(luminance, threshold=128):
    if luminance < threshold:
        return 0
    else:
        return 1

w, h = image.size
bw_values = []
for y in range(h):
    for x in range(w):
        grayscale_value = image.getpixel((x, y))
        bw = luminance_to_bw(grayscale_value, 128)
        bw_values.append(bw)

print(f"Black and white bitmap with {len(bw_values)} pixel values: {bw_values}")

bw_image = Image.new("1", (w, h))
bw_image.putdata(bw_values)
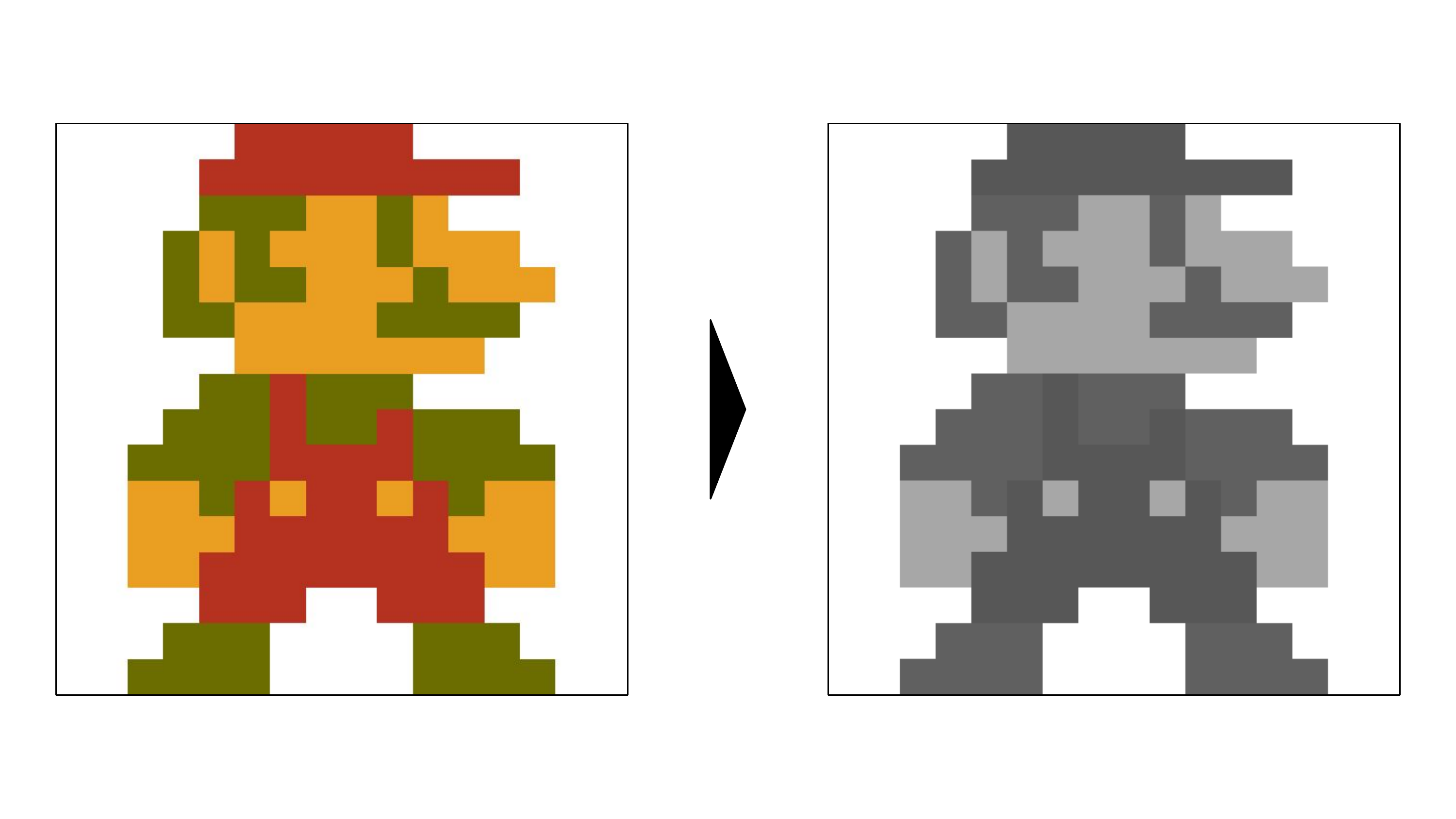
bw_image.save("xlsx/super_mario_bw.bmp")

Das Ergebnis seht ihr in Abbildung 4.27. Wie ihr sicher erkennt, verlieren wir auf dem Weg von Links nach Rehcts eine Menge Informationen.

4.9.4 Informationsverlust

Was fällt an der Kaskade von Farbe über Graustufen zu Schwarzweiß auf? Es geht eine Menge Information verloren.

  • In Farbe haben wir 256 Farbstufen pro Kanal, also über 16 Millionen mögliche Farben.
  • In Graustufen haben wir 256 Helligkeitswerte.
  • In Schwarzweiß bleiben nur noch 2 Zustände.

Mario ist am Ende zwar noch erkennbar, aber viele Details sind verloren gegangen. Besonders die seine Haut ist jetzt weiß und setzt sich nicht mehr vom Hintergrund ab. Wir könnten mit dem Schwellenwert experimentieren, aber mit nur zwei Farben bleibt die Darstellungsqualität stark begrenzt.

Eine wichtige Erkenntnis: Die Anzahl an Informationen im Bild (Farbtiefe und Auflösung) bestimmt maßgeblich die Qualität. Mehr Farben und mehr Pixel bedeuten ein detailreicheres Bild, aber auch größere Dateien. Dieser Trade-off zwischen Qualität und Größe begleitet uns überall in der Informatik.

Für Mario, der in seinem echten Klempnerdasein farbig ist, funktioniert die schwarzweiße Welt nicht gut. Wir nutzen deshalb für die Animation auf unserem Display eine Figur, die sowieso in Unifarbe daher kommt. Wenn ihr aber trotzdem mal ausprobieren wollt, wie Mario in Schwarzweiß auf dem Laufsteg aussieht, könnt ihr das gerne ausprobieren. Ihr findet die drei Bilder in dem zu diesem Buch gehörigen GitHub-Repository.

Für eine Animation auf unserem kleinen Display suchen wir uns eine Figur, die auch in Schwarzweiß gut funktioniert: Pacman.

4.10 Pacman

4.10.1 Von Farbe zu Schwarzweiß

Am Beispiel von Mario haben wir bereits eine Verarbeitungslogik von Farbe zu Schwarzweiß kennengelernt. Für Pacman können wir uns das Leben noch weiter vereinfachen.

Pacman ist ein weiterer Spieleklassiker aus den 1980er Jahren, mit dem ich meine ganz eigene Geschichte habe: Mein erstes größeres Programmierprojekt war die Entwicklung eines Pacman-Spiels in Turbo Pascal. Das ist 1998 während meines Ausslandsaufenthaltes in North Carolina in der elften Schulklasse entstanden. Für das Projekt habe ich Pacman Pixel für Pixel gezeichnet und animiert.

Das Spiel ist schnell erklärt. Pacman ist eine kreisförmige, gelbe Figur, die der Spieler durch ein Labyrinth steuert und dabei möglichst viele Punkte frisst. Währendessen wird Pacman von Geistern gejagt. Einen Eindruck vom Originalspiel seht ihr in Abbildung 4.28.

Wenn Pacman läuft, öffnet und schließt sich sein Mund im Wechsel. In Abbildung 4.29 seht ihr diese Mundbewegung in drei Bildern. Diese drei Sprites wollen wir im Folgenden auf unser Display übertragen.

Pacman von Farbe zu Schwarzweiß umzuwandeln ist denkbar einfach: Es gibt im Wesentlichen nur eine relevante Farbe (Gelb). Wir entscheiden also: Alle gelben Pixel werden weiß (1), alle anderen schwarz (0). Praktisch prüfen wir einfach, ob ein Pixel nicht weiß ist.

Wir laden zunächst das Bitmap-Bild von Pacman mit geschlossenem Mund und iterieren dann über alle Pixel, um die Schwarzweiß-Werte zu erzeugen:

from PIL import Image
image = Image.open("bmp/pacman_closed.bmp")

w, h = image.size
pacman_closed = []

for y in range(h):
    for x in range(w):
        r, g, b = image.getpixel((x, y))

        if r == 255 and g == 255 and b == 255:
            pacman_closed.append(0)
        else:
            pacman_closed.append(1)

print(pacman_closed)
1
Wir laden die Bitmap-Datei von Pacman mit geschlossenem Mund.
2
Wir lesen Breite und Höhe aus.
3
Wir erstellen eine Liste für die Schwarzweiß-Werte.
4
Zwei verschachtelte Schleifen iterieren über alle Pixelkoordinaten.
5
Wir lesen den RGB-Wert des aktuellen Pixels.
6
Ist das Pixel weiß, fügen wir eine 0 hinzu, sonst eine 1.

Die Logik in der Schleife ist einfach: Wenn alle Farbkomponenten den Wert 255 haben, dann ist das Pixel weiß und gehört somit nicht zu Pacman. Wir notieren also eine 0. Ansonsten ist das Pixel Teil von Pacman, und wir notieren eine 1.

Die Ausgabe in der letzten Zeile ist eine Liste, die etwa so aussieht:

[0, 0, 0, 0, 1, 1, 1, 1, ... 1, 1, 1, 1, 0, 0, 0, 0]

Genau dieses Format benötigen wir, um das Bild auf dem Display darzustellen. Perfekt!

Jetzt ergänzen wir wieder unseren Tinkerforge-Boilerplate und zeigen Pacman an:

from tinkerforge.ip_connection import IPConnection
from tinkerforge.bricklet_oled_128x64_v2 import BrickletOLED128x64V2

ipcon = IPConnection()
ipcon.connect('localhost', 4223)
oled = BrickletOLED128x64V2('25zo', ipcon)
oled.clear_display()

# Code zum Laden und Umwandeln des Bildes in Schwarzweiß (siehe oben)
...

oled.write_pixels(10, 10, 21, 22, pacman_closed)

Wir setzen Pacmans obere linke Ecke auf (10, 10). Pacman ist 12×13 Pixel groß, der untere rechte Eckpunkt ist also (21, 22). Wenn ihr das Programm ausführt, sollte Pacman mit geschlossenem Mund auf dem Display erscheinen (siehe Abbildung 4.30 (a)).

4.10.2 Pacman-Animation

Dasselbe Vorgehen können wir für die beiden anderen Bilder (halb geöffneter und geöffneter Mund) wiederholen. Anstatt den Code zu kopieren, kapseln wir die Umwandlung in eine Funktion:

from PIL import Image


def convert_rgb_to_bw(image_path):
    image = Image.open(image_path)
    w, h = image.size

    bw_values = []
    for y in range(h):
        for x in range(w):
            r, g, b = image.getpixel((x, y))

            if r == 255 and g == 255 and b == 255:
                bw_values.append(0)
            else:
                bw_values.append(1)

    return bw_values

Die Funktion convert_rgb_to_bw nimmt den Pfad eines Bildes entgegen, lädt es, wandelt alle Pixel in 0 oder 1 um und gibt die resultierende Liste zurück.

Wir rufen sie für alle drei Pacman-Bilder auf:

pacman_half = convert_rgb_to_bw("bmp/pacman_half.bmp")
pacman_closed = convert_rgb_to_bw("bmp/pacman_closed.bmp")
pacman_open = convert_rgb_to_bw("bmp/pacman_open.bmp")

Jetzt können wir die drei Bitmaps mit write_pixels() nacheinander anzeigen. Dazwischen legen wir kurze Pausen ein, damit unser Auge die Bilder wahrnehmen kann. Das Ganze läuft in einer Endlosschleife:

import time

wait_time = 0.1
while True:
    oled.write_pixels(10, 10, 21, 22, pacman_closed)
    time.sleep(wait_time)
    oled.write_pixels(10, 10, 21, 22, pacman_half)
    time.sleep(wait_time)
    oled.write_pixels(10, 10, 21, 22, pacman_open)
    time.sleep(wait_time * 2)
    oled.write_pixels(10, 10, 21, 22, pacman_half)
    time.sleep(wait_time)

Über die Variable wait_time könnt ihr die Geschwindigkeit der Animation steuern. In der letzten Phase (pacman_open) verdoppeln wir die Wartezeit, damit Pacman mit offenem Mund etwas länger sichtbar ist.

Abbildung 4.30: Die drei Pacman-Frames auf dem OLED-Display.

So sieht das Ganze als bewegtes Bild auf dem Display aus (siehe Abbildung 4.31):

In Listing 4.2 findet ihr den vollständigen Code für die Pacman-Animation, den ihr auch im GitHub-Repository findet:

Listing 4.2: Der vollständige Code für die Pacman-Animation
Code 
from tinkerforge.ip_connection import IPConnection
from tinkerforge.bricklet_oled_128x64_v2 import BrickletOLED128x64V2
import time
from PIL import Image

ipcon = IPConnection()
ipcon.connect("localhost", 4223)
oled = BrickletOLED128x64V2("<YOUR_UID>", ipcon)
oled.clear_display()

def convert_rgb_to_bw(image_path):
    image = Image.open(image_path)
    w, h = image.size

    bw_values = []
    for y in range(h):
        for x in range(w):
            r, g, b = image.getpixel((x, y))

            if r == 255 and g == 255 and b == 255:
                bw_values.append(0)
            else:
                bw_values.append(1)

    return bw_values

pacman_half = convert_rgb_to_bw("bmp/pacman_half.bmp")
pacman_closed = convert_rgb_to_bw("bmp/pacman_closed.bmp")
pacman_open = convert_rgb_to_bw("bmp/pacman_open.bmp")

wait_time = 0.1
while True:
    oled.write_pixels(10, 10, 21, 22, pacman_closed)
    time.sleep(wait_time)
    oled.write_pixels(10, 10, 21, 22, pacman_half)
    time.sleep(wait_time)
    oled.write_pixels(10, 10, 21, 22, pacman_open)
    time.sleep(wait_time * 2)
    oled.write_pixels(10, 10, 21, 22, pacman_half)
    time.sleep(wait_time)

Im echten Spiel bewegt Pacman nicht nur seinen Mund, sondern wandert durch das Labyrinth. Dafür müssten wir die Koordinaten des Rechtecks verändern und Pacman Pixel für Pixel über das Display bewegen. Ihr könnt das einmal selbst ausprobieren: Lasst Pacman von Links nach Rechts über den Bildschirm laufen. Wenn er am Ende angekommen ist, beginnt wieder von Vorne.

Für ein echtes Spiel müssten wir zusätzlich weitere Sprites für die Bewegungen in die anderen drei Richtungen erzeugen. Wenn Pacman nach rechts läuft, dann sollte er auch in die entsprechende Richtung blicken. Das selbe gilt für Oben und Unten. Das sparen wir uns an dieser Stelle, denn schließlich wollen wir kein komplettes Spiel entwickeln, sondern etwas über die Grundlagen moderner Computer lernen. Das haben wir hoffentlicht für das Theme Bilder heute geschafft.

Im nächsten Kapitel wenden wir uns wieder einem anderen spannenden Thema zu, das eine große Relevanz im Zusammenhang mit Computern hat: Töne und Klänge.